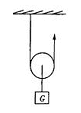
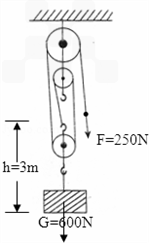
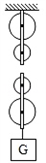
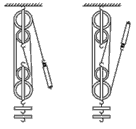
图甲是海洋中学科技小组设计的打捞水中物体的装置示意图。DB是以
(2)增大有用功在总功中所占的比例,在额外功不变的情况下,增大有用功的大小。
(3)换用最简单的机械。
滑轮组机械效率有关因素:
1、被提物体的重量,G越大,机械效率越高。
2、滑轮自重,滑轮组如果越多,虽然省力但是无用功多,机械效率越小。
3、绳与滑轮之间的摩擦。
无关因素:1、绕线方式,2、物体被提高的距离,3、提物体的速度。
考点名称:功率的计算公式的应用
单位时间里完成的,叫做功率,表示作功快慢程度的物理量,通常用P表示,故功率等于作用力与物体受力点速度的标量积。
功率的计算公式及单位
电功率计算公式:P=W/t =UI;在纯电阻电路中,根据欧姆定律U=IR代入P=UI中还可以得到:P=I²R=(U²)/R。
在动力学中:功率计算公式:1.P=W/t(平均功率)2.P=FV;P=Fvcosa(瞬时功率)
因为W=F(f力)×S(s位移)(功的定义式),所以求功率的公式也可推导出P=F·v:P=W /t=F*S/t=F*V(此公式适用于物体做匀速直线运动)
功率单位为瓦特,简称“瓦”,符号是“W”。W表示功,单位是“焦耳”,简称“焦”,符号是“J”。“t”表示时间,单位是“秒”,符号是“s”。
功率计算公式的应用
例1:用杠杆来撬一重为2400 N的大石块,当手在5 s内用300 N的力按杠杆,将杠杆一端压下1.6 m,大石块被举高多少m?人做功的功率为多大?(不计杠杆的重力和摩擦)
思路导航:(1)解答此题的关键是能够想到功的原理,往往有同学会用杠杆原理来解答此题,存在这种错误的同学主要是没有正确理解什么是力臂,题中给出的1.6 m是动力沿动力的方向通过的距离,而不是动力臂,题中要求的大石块被举高的高度恰好就是阻力沿阻力方向通过的距离。人对杠杆做的功即动力对杠杆做的功W1=Fs=300 N×1.6 m=480 J(注意:F和s对应),根据功的原理,W1=W2。
W2=G物h=2400 N×h. 480 J=2400×h,解得:h=0.2 m。
(2)人做功的功率就是动力做功的功率为96 W。
方法指导:利用杠杆做功时,在杠杆平衡的时候,根据功的原理和杠杆原理。
例2:关于功、功率,下列说法正确的是[ ]
A.机械的效率越高,做功越多
B.机械的效率越高,做功越快
C.机械的功率越大,做功越多
D.机械的功率越大,做功越快
思路导航:功率是表示做功的快慢,而不是做功多少的物理量;机械效率是表示有用功在总功中的比值,与做功的多少及功率的大小无关;所以本题的正确答案为D。
方法指导:这道题目包含了这章内容的三个重要的概念:功、功率、机械效率,只有真正理解了这些概念,才能准确的完成这道题。
例3:功率为30 kW,机械效率为60%的水泵,1 h内能把多少t的水从100 m深的矿井中抽到地面?(g取10 N/kg)
思路导航:本题既考查了功、功率、时间的关系,又考查了总功、有用功和机械效率的关系,利用水泵的功率,工作时间可以求出所做的总功W总=Pt,根据有用功、总功、机械效率的关系可以求出有用功W有=W总η,结合有用功的意义,在这里水泵对水所做的功就是有用功,即W有=G水h,这样就可以求出水的质量,解答过程如下:
W总=Pt=3×104 W×3600 s=1.8×108 J
W有=W总η=1.08×108 J×0.6=6.48×107 J(注意单位时统一)
W有=G水h
G水=6.48×105 N
m水=6.48×104 kg=64.8 t
方法指导:根据题中所给的已知条件来确定要选用的公式,同一个物理量可以通过好多途径来求,这就要求我们把学过的知识要能紧紧地联系在一起,做到灵活运用,融会贯通。
考点名称:杠杆的平衡条件
杠杆的平衡条件:
杠杆的平衡条件是:动力X动力臂=阻力X阻力臂
或
这个平衡条件也就是阿基米德发现的杠杆原理。
上面的关系式也可以写成下面的形式:

杠杆的定义:
只要在力的作用下能够绕支撑点转动的坚实物体都是杠杆。跷跷板、剪刀、扳子、撬棒等,都是杠杆。
杠杆的五要素:
(1)杠杆转动时绕着的固定点叫支点;
(2)使杠杆转动的力叫动力;
(3)阻碍杠杆转动的力叫阻力;
(4)从支点到动力作用线的距离叫动力臂;
(5)从支点到阻力作用线的距离叫阻力臂.
杠杆的原理:
主条目:力矩当杠杆处于静止状态或匀速转动状态时,杠杆就处于平衡状态。
杠杆的平衡条件:动力×动力臂=阻力×阻力臂
用字母表示就是:F1×L1=F2×L2
杠杆的平衡条件又叫杠杆原理,是阿基米德最早提出的。据此他发出了给我一个支点,我可以撬动地球。的豪言壮语、
杠杆的分类:
一类:支点在动力点和阻力点的中间。称为第一类杠杆。既可能省力的,也可能费力的,主要由支点的位置决定,或者说由臂的长度决定。例:跷跷板,剪刀,船桨,(运煤气罐等重物的)手推车,鞋拔子,塔吊,撬钉扳手等。
二类:阻力点在动力点和支点中间。称为第二类杠杆。由于动力臂总是大于阻力臂,所以它是省力杠杆。例:坚果夹子,门,钉书机,跳水板,扳手,开(啤酒)瓶器,(运水泥、砖的)手推车。
三类:动力点在支点和阻力点之间。称为第三类杠杆。特点是动力臂比阻力臂短,所以这类杠杆是费力杠杆,然而能够节省距离。例:镊子,手臂,鱼竿,皮划艇的桨,下颚,锹、扫帚、球棍等以一手为支点,一手为动力的器械。
另外,像轮轴这类的工具也属于一种变形杠杆。就拿最简单、相似于第一类杠杆的定滑轮来介绍,滑轮轴心好比支点,两端物体的拉力好比杠杆的两端施力,而如果滑轮是一个完美的圆,施力臂和阻力臂皆将是圆的半径。
利用杠杆平衡条件来分析和计算有关问题,一般遵循以下步骤:
(1)确定杠杆支点的位置。
(2)分清杠杆受到的动力和阻力,明确其大小和方向,并尽可能地作出力的示意图。
(3)确定每个力的力臂。
(4)根据杠杆平衡条件列出关系式并分析求解。
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
| [高考] 2022 西安电子科技大学《软件工程》大作业答案 (2022-04-25) |
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |