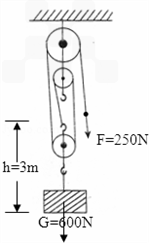
中华神州打捞公司用如图所示的滑轮组,打捞沉在长江三峡江底一个
考点名称:浮力及阿基米德原理
浮力:物理学名词,一般指物体浸泡(包含)在液体或气体中产生的托力,是物体在流体(包括液体和气体)中,上下表面所受的压力差。船能在水面上漂浮,就是因为浮力的作用。
浮力产生的原因:
浮力是由于周围液体对物体上、下表面的作用存在压力差而产生的。如图所示,浸没在液体中的立方体,左右两侧面,前后两侧面所受水的压力大小相等,方向相反,彼此平衡。而上、下两表面处的液体中不同深度,所受到的液体的压强不同,因受力面积相等,所以压力不相等。下表面所受到的竖直向上的压力大于上表面所受到的竖直向下的压力,因而产生了浮力,所以浮力的方向总是竖直向上的,即F浮=F向上一F向下。

(1)当物体上表面露出液面时,F向下=0,则F浮=F向上。如:物体漂浮时,受到的浮力等于液体对它向上的压力。
(2)浸在液体中的物体不一定都受到浮力。如:桥墩、拦河坝等因其下底面同河床紧密黏合,水对它向上的压力F向上=0,故物体不受浮力作用。可见产生浮力的必要条件是:F浮=F向上—F向下>0,即F向上>F向下。当F向上=0或F向上≤F向下时,物体不受浮力作用。
(3)同一物体浸没在液体的不同深度,所受的压力差不变,浮力不变。
(4)浮力的实质是液体对物体各个表面压力的合力。因此,在分析物体的受力情况时,浮力和液体的压力不能同时考虑。
影响浮力大小的因素:
有关浸在液体中的物体受到浮力的大小,跟物体浸入液体中的体积有关,跟液体的密度有关,跟物体浸入液体中的深度无关,跟物体本身密度大小无关。
阿基米德原理:
浸入液体里的物体受到向上的浮力,浮力的大小等于它排开的液体受到的重力,这就是著名的阿基米德原理,也是是物理学中力学的一条基本原理。
阿基米德原理公式表示如下:F浮=G排=ρ液*gV排,浮力大小只与ρ液、V排有关浮力的大小只与液体的密度、排开液体的体积有关,而与物体浸入液体的深度没有关系。
阿基米德原理不仅适用于所有液体,而且也广泛地适用在一切气体中..对于浸入液体的物体,只要知道ρ液、V排,我们就能求出浮力,阿基米德原理是计算浮力最普遍适用的规律.
阿基米德原理的五点透析:
(1)原理中所说的“浸在液体里的物体”包含两种状态:一是物体的全部体积都浸入液体里,即物体浸没在液体里;二是物体的一部分体积浸入液体里,另一部分露在液面以上。
(2)G排指被物体排开的液体所受的重力,F浮= G排表示物体受到的浮力的大小等于被物体排开的液体的重力。
(3)V排是表示被物体排开的液体的体积,当物体全部浸没在液体里时,V排=V物。
(4)由可以看出,浮力的大小只跟液体的密度和物体排开液体的体积这两个因素有关,而跟物体本身的体积、密度、形状、在液体中的深度、液体的多少等因素无关。
(5)阿基米德原理也适用于气体,但公式中ρ液应该为ρ气。
考点名称:滑轮(组)中拉力的计算
滑轮组是由若干个定滑轮和动滑轮匹配而成,可以达到既省力又改变力作用方向的目的。使用中,省力多少和绳子的绕法,决定于滑轮组的使用效果。动滑轮被两根绳子承担,即每根绳承担物体和动滑轮。
滑轮有两种:定滑轮和动滑轮 ,组合成为滑轮组。
(1)定滑轮,
定滑轮实质是等臂杠杆,不省力也不费力,但可以改变作用力方向.
定滑轮的特点
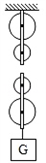
通过定滑轮来拉钩码并不省力。通过或不通过定滑轮,弹簧秤的读数是一样的。可见,使用定滑轮不省力但能改变力的方向。在不少情况下,改变力的方向会给工作带来方便。
定滑轮的原理
定滑轮实质是个等臂杠杆,动力L1、阻力L2臂都等于滑轮半径。根据杠杆平衡条件也可以得出定滑轮不省力的结论;
(2)动滑轮
动滑轮实质是动力臂为阻力臂二倍的杠杆,省1/2力多费1倍距离.
动滑轮的特点
使用动滑轮能省一半力,费距离。这是因为使用动滑轮时,钩码由两段绳子吊着,每段绳子只承担钩码重的一半。使用动滑轮虽然省了力,但是动力移动的距离大于钩码升高的距离,即费了距离。
动滑轮的原理
动滑轮实质是个动力臂(L1),为阻力臂(L2)二倍的杠杆;
(3)滑轮组
滑轮组:由定滑轮跟动滑轮组成的滑轮组,既省力又可改变力的方向.
滑轮组用几段绳子吊着物体,提起物体所用的力就是总重的几分之一.绳子的自由端绕过动滑轮的算一段,而绕过定滑轮的就不算了.
使用滑轮组虽然省了力,但费了距离,动力移动的距离大于重物移动的距离.
滑轮组的用途:
为了既节省又能改变动力的方向,可以把定滑轮和动滑轮组合成滑轮组。
滑轮组的省力情况:
使用滑轮组时,滑轮组由几段绳子吊着动滑轮,提起物体所用的力就是物重的几分之一。
滑轮组由几股绳子承担物重:
有几股绳与动滑轮相连,承担物重的绳子的股数n 就是几,而重物上升的高度h与绳子自由端移动的距离s的关系是:s=nh。如图:在动、定滑轮之间画一条线,将它们分开,只算在动滑轮上的绳子的股数。

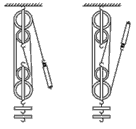
例1如图甲、乙滑轮组装置,所有摩擦不计,分别用F1、F2竖直匀速拉动重物G,已知每个滑轮重力为 G/2,则力F1和F2之比为( )

A.1:1B.3:2C.2:3D.3:4
解析:当考虑动滑轮的重力,不计摩擦时,F= ,由图中滑轮组的绕线方法可知:F1=
,由图中滑轮组的绕线方法可知:F1=
 。
。
答案:C
滑轮组省力情况的判断
1.滑轮组竖放:若不考虑动滑轮自重以及绳、轮摩擦,滑轮组用几股绳子吊着物体,提起物体所用的动力就是物重的几分之一,即 ;若考虑动滑轮自重,但忽略摩擦,此式变为F拉=
;若考虑动滑轮自重,但忽略摩擦,此式变为F拉=  。用“连动法”,弄清直接与动滑轮连接的绳子的根数n,在图甲中我们以重物和动滑轮为研究对象,n=4,有四根绳子承担动滑轮及重物,所以用力
。用“连动法”,弄清直接与动滑轮连接的绳子的根数n,在图甲中我们以重物和动滑轮为研究对象,n=4,有四根绳子承担动滑轮及重物,所以用力 。同理,分析乙图可知,提起重物及动滑轮的
。同理,分析乙图可知,提起重物及动滑轮的 。
。

2.滑轮组横放:在不考虑绳、轮摩擦时,滑轮组用几股绳拉着物体做匀速直线运动,拉力大小就是物体所受摩擦力的几分之一,即: 。
。
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
| [高考] 2022 西安电子科技大学《软件工程》大作业答案 (2022-04-25) |
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |