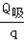某太阳能热水器内装0.8m3的水.夏天天晴时,这个热水器接受阳光照
(1)ρ一定时,m和V成正比;(因为ρ=m/V,ρ一定,m增大,V也增大,所以成正比)
(2)m一定时,ρ与V成反比;(因为m=ρv,m一定,v增大,ρ变小,所以成反比)
(3)V一定时,ρ与m成正比。
结合物理意义,三种情况只有(1)的说法正确,(2)(3)都是错误的。
因为同种物质的密度是一定的,它不随体积和质量的变化而变化,所以在理解物理公式时,不可能脱离物理事实,不能单纯地从数学的角度理解物理公式中各量的关系。
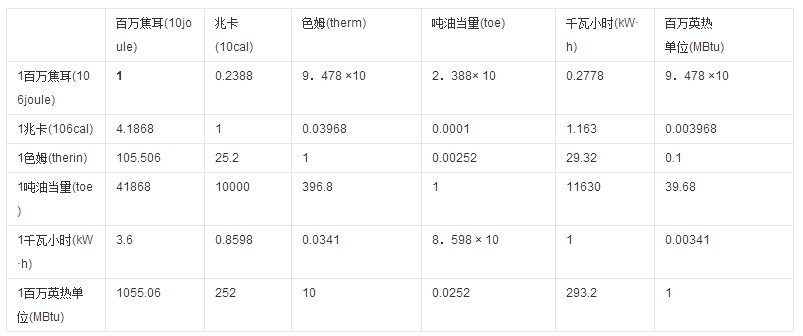
常用气体密度换算:
1.干空气密度
密度是指单位体积空气所具有的质量, 国际单位为千克/米3(kg/m3 ),一般用符号ρ表示。其定义式为: ρ = M/V (1--1)
式中 M——空气的质量,kg;
V——空气的体积,m3。
空气密度随空气压力、温度及湿度而变化。上式只是定义式,通风工程中通常由气态方程求得干、湿空气密度的计算式。由气态方程有:
ρ=ρ0*T0*P/P0*T (1--2)
式中 :ρ——其它状态下干空气的密度,kg/m3;
ρ0——标准状态下干空气的密度,kg/m3;
P、P0——分别为其它状态及标准状态下空气的压力,千帕(kpa);
T、T0——分别为其它状态及标准状态下空气的热力学温度,K。
标准状态下,T0=273K,P0=101.3kPa时,组成成分正常的干空气的密度ρ0=1.293kg/m3。将这些数值代入式(1-2),即可得干空气密度计算式为:
ρ = 3.48*P/T(1--3)
使用上式计算干空气密度时,要注意压力、温度的取值。式中P为空气的绝对压力,单位为kPa;T为空气的热力学温度(K),T=273+t, t为空气的摄氏温度(℃)。
2.湿空气密度
对于湿空气,相当于压力为P的干空气被一部分压力为Ps的水蒸汽所占据,被占据后的湿空气就由压力为Pd的干空气和压力为Ps的水蒸汽组成。根据道尔顿分压定律,湿空气压力等于干空气分压Pd与水蒸汽分压Ps之和,即:P=Pd+Ps。
根据相对湿度计算式,水蒸汽分压Ps=ψPb,根据气态方程及道尔顿的分压定律,即可推导出湿空气密度计算式为:
ρw=3.48*P(1-0.378*ψ*Pb/P)/T (2--1)
式中 ρw ——湿空气密度,kg/m3;
ψ——空气相对湿度,%;
Pb——饱和水蒸汽压力,kPa(由表2-1-1确定)。
其它符号意义同上。
密度公式的应用:
1. 有关密度的图像问题
此问题一般是给出质量一体积图像,判断或比较物质密度。解答时可在横坐标(或纵坐标)任选一数值,然后在纵坐标(或横坐标)上找到对应的数值,进行分析比较。
例1如图所示,是甲、乙两种物质的m一V图像,由图像可知( )
A.ρ甲>ρ乙
B.ρ甲=ρ乙
C.ρ甲<ρ乙
D.无法确定甲、乙密度的大小

解析:要从图像直接看出甲、乙两种物质的密度大小目前还做不到,我们要先借助图像,根据公式ρ = 总结规律后方可。
总结规律后方可。
如图所示,在横轴上任取一点V0,由V0作横轴的垂线V0B,分别交甲、乙两图线于A、B两点,再分别从A、B两点作纵轴垂线,分别交纵轴于m甲、m乙两点。则甲、乙两种物质的密度分别为 ,ρ乙=
,ρ乙=  ,因为m甲<m乙,所以ρ甲<ρ乙,故C正确。
,因为m甲<m乙,所以ρ甲<ρ乙,故C正确。

2. 密度公式ρ = 及变形
及变形 、m=ρV的应用:
、m=ρV的应用:
密度的公式是ρ = ,可得出质量计算式m=ρV 和体积计算式
,可得出质量计算式m=ρV 和体积计算式 。只要知道其中两个物理量,就可以代入相应的计算式进行计算。审题时注意什么量是不变的,什么量是变化的。
。只要知道其中两个物理量,就可以代入相应的计算式进行计算。审题时注意什么量是不变的,什么量是变化的。
例2某瓶氧气的密度是5kg/m3,给人供氧用去了氧气质量的一半,则瓶内剩余氧气的密度是_____;容积是10L的瓶子装满了煤油,已知煤油的密度是 0.8×103kg/m3,则瓶内煤油的质量是_____,将煤油倒去4kg后,瓶内剩余煤油的密度是______。
解析:氧气用去一半,剩余部分仍然充满整个氧气瓶,即质量减半体积不变,所以氧气的密度变为 2.5kg/m3。煤油倒去一半后,体积质量同时减半,密度不变。
答案:2.5kg/m3;8kg;0.8×10kg/m3。
3. 比例法求解物质的密度
利用数学的比例式来解决物理问题的方法称之为 “比例法”。能用比例法解答的物理问题具备的条件是:题目所描述的物理现象,由初始状态到终结状态的过程中至少有一个量保持不变,这个不变的量是由初始状态变成终结状态的桥梁,我们称之为“中介量”。
例3甲、乙丽个物体的质量之比为3:2,体积之比为l:3,那么它们的密度之比为( )
A.1:2B.2:1C.2:9D.9:2
解析:(1)写出所求物理量的表达式: ,
,
(2)写出该物理量比的表达式:

(3)化简:代入已知比值的求解:

密度、质量、体积计算中的“隐含条件” 问题:
很多物理问题中的有些条件需要仔细审题才能确定,这类条件称为隐含条件。因此寻找隐含条件是解决这类问题的关键。以密度知识为例,密度计算题形式多样,变化灵活,但其中有一些题具有这样的特点:即质量、体积、密度中的某个量在其他量发生变化时保持不变,抓住这一特点,就掌握了求解这类题的规律。
1.隐含体积不变
例1一个瓶子最多能装0.5kg的水,它最多能装_____kg的水银,最多能装_____m3的酒精。 ρ水银=13.6×103kg/m3,ρ水=1.0×103kg/m3,ρ酒精= 0.8×103kg/m3)
解析:最多能装即装满瓶子,由最多装水量可求得瓶子的容积为V=5×10-4m3,则装水银为m水银=13.6×103kg/m3×5×10-4m3=6.8kg。装酒精的体积为瓶子的容积。
答案6.8;5×10-4
2. 隐含密度不变
例2一块石碑的体积为V样=30m3,为测石碑的质量,先取了一块刻制石碑时剔下来的小石块作为样品,其质量是m样=140g,将它放入V1=100cm3的水中后水面升高,总体积增大到V2=150cm3,求这块石碑的质量m碑。
解析:此题中隐含的条件是石碑和样品是同种物质,密度相同,而不同的是它们的体积和质量。依题意可知,样品体积为:
V样=V2-V1=150cm3一100cm3=50cm3 =5.0×10
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
| [高考] 2022 西安电子科技大学《软件工程》大作业答案 (2022-04-25) |
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |