(10分)一个有一定厚度的圆盘,可以绕通过中心垂直于盘面的水平轴转动,圆盘加速转动时,角速度的增加量Δω与对应之间Δt的比值定义为角加速度β(即)。我们用电磁打点计时器、米
◎ 题目
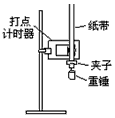
(10分)一个有一定厚度的圆盘,可以绕通过中心垂直于盘面的水平轴转动,圆盘加速转动时,角速度的增加量Δω与对应之间Δt的比值定义为角加速度β(即  )。我们用电磁打点计时器、米尺、游标卡尺、纸带、复写纸来完成下述实验:(打点计时器所接交流电的频率为50Hz,A、B、C、D……为计数点,相邻两计数点间有四个点未画出) )。我们用电磁打点计时器、米尺、游标卡尺、纸带、复写纸来完成下述实验:(打点计时器所接交流电的频率为50Hz,A、B、C、D……为计数点,相邻两计数点间有四个点未画出)①如图甲所示,将打点计时器固定在桌面上,将纸带的一端穿过打点计时器的限位孔,然后固定在圆盘的侧面,当圆盘转动时,纸带可以卷在圆盘侧面上;  ②接通电源,打点计时器开始打点,启动控制装置使圆盘匀加速转动; ③经过一段时间,停止转动和打点,取下纸带,进行测量。 (1)用20分度的游标卡尺测得圆盘的半径如图乙所示,圆盘的半径r为 cm; (2)由图丙可知,打下计数点D时,圆盘转动的角速度为 rad/s; (3)纸带运动的加速度大小为 m/s2,圆盘转动的角加速度大小为 rad/s2; (4)如果实验测出的角加速度值偏大,其原因可能是 (至少写出1条)。 |
◎ 答案
(1)6.000cm;(2)6.5rad/s;(3)0.59m/s2,9.8rad/s2;(4)存在空气阻力;纸带与限位孔之间存在摩擦力等。 |
◎ 解析
分析:(1)20分度的游标卡尺精确度为0.05mm,读数时先读大于1mm的整数部分,再读不足1m的小数部分; (2)根据平均速度等于中间时刻瞬时速度求出D点的瞬时速度,然后根据v=ωr求解角速度; (3)用逐差法求解出加速度,再根据加速度等于角加速度与半径的乘积来计算角加速度; (4)根据公式ρ=ar进行判断. 解:(1)整数部分为60mm,小数部分为零,由于精确度为0.05mm,故需写到0.001cm处,故读数为6.000cm; 故答案为:6.000; (2)打下计数点D时,速度为 vD=  = = =0.389m/s =0.389m/s故 ω=  = = ≈6.5rad/s ≈6.5rad/s故答案为:6.5; (3)纸带运动的加速度为 a=  = = = = =0.59m/s2 =0.59m/s2由于ρ=  ,ω= ,ω= ,故角加速度为ρ= ,故角加速度为ρ= = = ≈0.98rad/s2 ≈0.98rad/s2故答案为:0.59,0.98; (4)根据公式ρ=  ,ρ偏大,为a偏大,或者r偏小,故可能的原因为:测量转动半径时没有考虑纸带的厚度. ,ρ偏大,为a偏大,或者r偏小,故可能的原因为:测量转动半径时没有考虑纸带的厚度. |
◎ 知识点
专家分析,试题“(10分)一个有一定厚度的圆盘,可以绕通过中心垂直于盘面的水平轴转动,圆盘加速转动时,角速度的增加量Δω与对应之间Δt的比值定义为角加速度β(即)。我们用电磁打点计时器、米…”主要考查了你对 【实验:探究小车速度随时间变化的规律】,【实验:探究弹力与弹簧伸长的关系】,【实验:探究加速度与力、质量的关系】,【实验:探究功与速度变化的关系】 等知识点的理解和应用能力。关于这些知识点的“档案”,你可以点击相应的链接进行查看和学习。- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
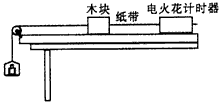
上一篇:某同学设计了一个探究加速度a与物体所受合力F及质量m关系的实验,如图所示,图甲为实验装置简图.(交流电的频率为50Hz)(1)图乙为某次实验得到的纸带,根据纸带可求出小车的加速
下一篇:研究小车的匀变速运动,记录纸带如图所示,图中两计数点间有四个点未画出.已知打点计时器所用电源的频率为50Hz,则小车运动的加速度a=________m/s2,打P点时小车运动的v=___
零零教育社区:论坛热帖子
| [高考] 2022 西安电子科技大学《软件工程》大作业答案 (2022-04-25) |
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |

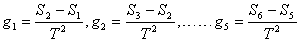
![下列能源在利用中,最环保的是[]A.太阳能B.石油C.煤D.核能](http://www.00-edu.com/d/file/2022-07-30/202e1b1a2d8d8ff82833405f33b8b771.gif)
