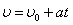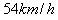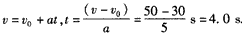A、B两站相距x,将其分成n段,汽车无初速由A站出发,分n段向B站做匀加速直线运动,第一段的加速度为a.当汽车到达每一等份的末端时,其加速度增加an,则汽车到达B站时的速度为
◎ 题目
A、B两站相距x,将其分成n段,汽车无初速由A站出发,分n段向B站做匀加速直线运动,第一段的加速度为a.当汽车到达每一等份的末端时,其加速度增加
|
◎ 答案
| 设汽车到达第n段末端速度为vn, 根据位移速度关系式得:v12-02=2a
v22-v12=2a(1+
v32-v22=2a(1+2
v42-v32=2a(1+3
… vn2-v(n-1)2=2a【1+(n-1)
把上面各式相加得:vn2=
解得:vn=
故答案为:
|
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
上一篇:一个滑雪人,从85m长的山坡上匀加速滑下,初速度是1.8m/s,滑到山坡底端的末速度是5.0m/s,求:(1)下滑过程中的平均速度.v;(2)下滑的加速度a;(3)下滑的时间t.
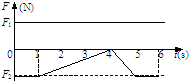
下一篇:在火车站站台上有一观察者,在列车开动时恰好站在第一节车厢的最前端,列车起动后做匀加速直线运动.5s末时第一节车厢末端通过观察者(每节车厢等长)则:(1)从开始观察经过____
零零教育社区:论坛热帖子
| [高考] 2022 西安电子科技大学《软件工程》大作业答案 (2022-04-25) |
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |