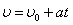如图所示,斜面倾角为θ,一块质量为m、长为l的匀质板放在很长的斜面上,板的左端有一质量为M的物块,物块上连接一根很长的细绳,细绳跨过位于斜面顶端的光滑定滑轮并与斜面平
◎ 题目
| 如图所示,斜面倾角为θ,一块质量为m、长为l的匀质板放在很长的斜面上,板的左端有一质量为M的物块,物块上连接一根很长的细绳,细绳跨过位于斜面顶端的光滑定滑轮并与斜面平行,开始时板的右端距离斜面顶端足够远.试求: (1)若板与斜面间光滑,某人以恒力F竖直向下拉绳,使物块沿板面由静止上滑过程中,板静止不动,求物块与板间动摩擦因数μ0; (2)在(1)情形下,求物块在板上滑行所经历的时间t0; (3)若板与物块和斜面间均有摩擦,且M=m,某人以恒定速度v=
 |
◎ 答案
  (1)分别对物块和木板受力分析并建立如图所示的直角坐标系, 对木块M:G1=Mg,则:F1=Mgcosθ, 又:M在Y轴方向受力平衡, 所以F3=F1=Mgcosθ. 又:f=μ0F1=μ0Mgcosθ 对板m:因为静止,所以X、Y方向分别受力平衡: X轴方向:F5=G2sinθ=mgsinθ;f=μ0Mgcosθ; 所以:mgsinθ=μ0Mgcosθ; 得:μ0=
(2)设物块M的加速度为a0,物块Y方向合力为零,所以合力即为X轴上的合力: X轴方向:F2=G1sinθ=Mgsinθ;f=μ0Mgcosθ; 所以:F合=F-Mgsinθ-μ0Mgcosθ 由牛顿第二定律:F=ma得: F-Mgsinθ-μ0Mgcosθ=Ma0 即:a0=
又:l=
联立解得:t0=
(3)设物块在板上滑行的时间为t1,板的加速度为a,  对板有:Y方向合力为零,所以合力即为X方向的合力: X轴方向:f=μ1Mgcosθ;f1=μ2(M+m)gcosθ;F5=G2sinθ=mgsinθ 所以:F合=μ1Mgcosθ-mgsinθ-μ2(M+m)gcosθ 由牛顿第二定律:F=ma得: μ1Mgcosθ-mgsinθ-μ2(M+m)gcosθ=ma① 且物块最终不滑离板的右端.说明物块和木板最终要达到相同的速度v:所以有:v=at1② ①②联立解得 t1=
又设物块从板的左端运动到右端的时间为t2, 则:vt2-
t2=
为使物块最终不滑离板的右端,必须满足 t1≤t2 即 |