在一次抗洪救灾工作中,一架直升机A用长H=50m的悬索(重力可忽略不计)系住一质量m=50kg的被困人员B,直升机A和被困人员B以v0=10m/s的速度一起沿水平方向匀速运动,如图甲所示
◎ 题目
| 在一次抗洪救灾工作中,一架直升机A用长H=50m的悬索(重力可忽略不计)系住一质量m=50kg的被困人员B,直升机A和被困人员B以v0=10m/s的速度一起沿水平方向匀速运动,如图甲所示.某时刻开始收悬索将人吊起,在5s时间内,A、B之间的竖直距离以l=50-t2(单位:m)的规律变化,取g=10m/s2. (1)求这段时间内悬索对被困人员B的拉力大小. (2)求在5s末被困人员B的速度大小及位移大小. (3)直升机在t=5s时停止收悬索,但发现仍然未脱离洪水围困区,为将被困人员B尽运送到安全处,飞机在空中旋转后静止在空中寻找最近的安全目标,致使被困人员B在空中做圆周运动,如图乙所示.此时悬索与竖直方向成37°角,不计空气阻力,求被困人员B做圆周运动的线速度以及悬索对被困人员B的拉力.(sin 37°=0.6,cos 37°=0.8) 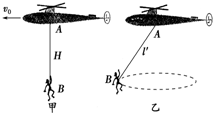 |
◎ 答案
| (1)根据l=50-t2知,被困人员向上的加速度a=2m/s2. 根据牛顿第二定律得,F-mg=ma 得,F=mg+ma=600N. 故内悬索对被困人员B的拉力大小为600N. (2)5s末在水平方向上的位移x=v0t=50m 速度不变v0=10m/s/ 在竖直方向上的位移y=
速度vy=at=10m/s 所以v=
位移s=
故5s末被困人员B的速度大小及位移大小分别为10
(3)被困人员受重力和拉力,两个力的合力提供圆周运动所需的向心力.受力如图. 有Tcosθ=mg.所以拉力T=
mgtanθ=m
解得v= |

![某质点的位移随时间的变化关系式x=4t-2t2,x与t的单位分别是m和s。则该质点的初速度和加速度分别是[]A.4m/s和-2m/s2B.0和2m/s2C.4m/s和-4m/s2D.4m/s和0](http://www.00-edu.com/d/file/2022-08-02/623667c33164cc94e562904501d00dac.png)
![在平直公路上,自行车与同方向行驶的一辆汽车在t=0时同时经过某一个路标,它们的位移xm随时间ts变化的规律为:汽车为,自行车为,则下列说法正确的是[]A.汽车作减速直线运动,](http://www.00-edu.com/d/file/2022-08-02/c6601189f5f4ab22548fe82420a0312c.gif)
![一初速度为6m/s做直线运动的质点,受到力F的作用产生一个与初速度方向相反、大小为2m/s2的加速度,当它的位移大小为3m时,所经历的时间可能为[]A.B.C.sD.s](http://www.00-edu.com/d/file/2022-08-02/68dc25bf024f69fcc1ae788014dcd0b6.gif)

