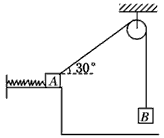
如图所示,按顺时针方向在竖直平面内作匀速转动的轮子边缘上有一点A.当A通过与圆心等高的a点时,有一质点B从圆心O开始做自由落体运动.已知圆的半径为R,求:(1)轮子的角速度ω
◎ 题目
| 如图所示,按顺时针方向在竖直平面内作匀速转动的轮子边缘上有一点A.当A通过与圆心等高的a点时,有一质点B从圆心O开始做自由落体运动.已知圆的半径为R,求: (1)轮子的角速度ω满足什么条件时,点A才能与B相遇? (2)轮子的角速度ω满足什么条件时,点A与B的速度才会相同?  |
◎ 答案
(1)质点从B点做自由落体运动,根据R=
t=
A和B只能在d点相遇,所以A运动的时间为(n+
所以(n+
解得:ω=2π(n+
(2)点A与B的速度相同的位置只能在c点, 则t=(n+1)T, 根据速度相等有:ωR=gt=g(n+1)
解得:ω=
答:(1)轮子的角速度ω=2π(n+
|


![关于自由落体运动,下面说法正确的是[]A.它是竖直向下,v0=0,a=g的匀加速直线运动B.在开始连续的三个1s内通过的位移之比是1:3:5C.在开始连续的三个1s末的速度大小之比是1:2](http://www.00-edu.com/d/file/2022-09-04/f124a826fe51a38d083a0ad77f6e56bc.gif)