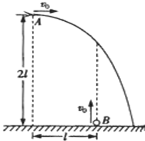
有一竖直放置、两端封闭的长玻璃管,管内为真空,管内有一小球自某处自由下落(初速度为零),落到玻璃管底部时与底部发生弹性碰撞.以后小球将在玻璃管内不停地上下跳动.现用支
◎ 题目
有一竖直放置、两端封闭的长玻璃管,管内为真空,管内有一小球自某处自由下落(初速度为零),落到玻璃管底部时与底部发生弹性碰撞.以后小球将在玻璃管内不停地上下跳动.现用支架固定一照相机,用以拍摄小球在空间的位置.每隔一相等的确定的时间间隔T拍摄一张照片,照相机的曝光时间极短,可忽略不计.从所拍到的照片发现,每张照片上小球都处于同一位置.求小球开始下落处离玻璃管底部距离(用H表示)的可能值以及与各H值相应的照片中小球位置离玻璃管底部距离的可能值. |
◎ 答案
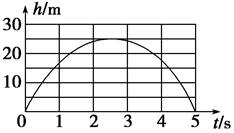
小球沿竖直线上下运动时,其离开玻璃管底部的距离h随时间t变化的关系如图所示.设照片拍摄到的小球位置用A表示,A离玻璃管底部的距离为hA,小球开始下落处到玻璃管底部的距离为H.小球可以在下落的过程中经过A点,也可在上升的过程中经过A点.现以τ表示小球从最高点(即开始下落处)落到玻璃管底部所需的时间(也就是从玻璃管底部反跳后上升到最高点所需的时间),τ1表示小球从最高点下落至A点所需的时间(也就是从A点上升至最高点所需的时间),τ2表示小球从A点下落至玻璃管底部所需的时间(也就是从玻璃管底部反跳后上升至A点所需的时间).显然,τ1+τ2=τ.根据题意,在时间间隔T 的起始时刻和终了时刻小球都在A点.用n表示时间间隔 T 内(包括起始时刻和终了时刻)小球位于A点的次数(n≥2).下面分两种情况进行讨论: 1.A点不正好在最高点或最低点. 当n为奇数时有 T=(n-1)τ1+(n-1)τ2=(n-1)τ n=3,5,7,…(1) 在(1)式中,根据题意τ1可取0<τ1<τ中的任意值,而 τ2=τ-τ1 (2) 当n为偶数时有 T=nτ2+(n-2)τ1=nτ1+(n-2)τ2 n=2,4,6,…(3) 由(3)式得τ1=τ2 (4) 由(1)、(3)、(4)式知,不论n是奇数还是偶数,都有 T=(n-1)τ n=2,3,4,…(5) 因此可求得,开始下落处到玻璃管底部的距离的可能值为 Hn=
若用Hn表示与n对应的H值,则与Hn相应的A点到玻璃管底部的距离 hA=Hn-
当n为奇数时,τ1可取0<τ1<τ中的任意值,故有 0<hA<Hn[Hn=
可见与Hn相应的hA的可能值为0与Hn之间的任意值. 当n为偶数时,τ1=
hA=
2.若A点正好在最高点或最低点. 无论n是奇数还是偶数都有 T=2(n-1)τ n=2,3,4,???(10) Hn=
|