质量为M的平板车P高h,质量为m的小物块Q的大小不计,位于平板车的左端,系统原来静止在光滑水平面地面上.一不可伸长的轻质细绳长为R,一端悬于Q正上方高为R处,另一端系一质
◎ 题目
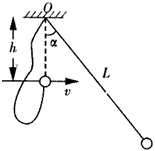
| 质量为M的平板车P高h,质量为m的小物块Q的大小不计,位于平板车的左端,系统原来静止在光滑水平面地面上.一不可伸长的轻质细绳长为R,一端悬于Q正上方高为R处,另一端系一质量也为m的小球(大小不计).今将小球拉至悬线与竖直位置成60°角,由静止释放,小球到达最低点时与Q的碰撞时间极短,且无能量损失,已知Q离开平板车时速度大小是平板车速度的两倍,Q与P之间的动摩擦因数为μ,M:m=4:1,重力加速度为g.求: (1)小物块到达最低点与Q碰撞之前瞬间的速度是多大? (2)小物块Q离开平板车时平板车的速度为多大? (3)平板车P的长度为多少? (4)小物块Q落地时距小球的水平距离为多少?  |
◎ 答案
| (1)、小球由静止摆到最低点的过程中,机械能守恒,则有: mgR(1-cos60°)=
∴解得小物块到达最低点与Q碰撞之前瞬间的速度是: v0=
(2)、小球与物块Q相撞时,没有能量损失,满足动量守恒,机械能守恒,则知: mv0=mv1+mvQ
由以上两式可知二者交换速度:v1=0,vQ=v0=
小物块Q在平板车上滑行的过程中,满足动量守恒,则有: mvQ=Mv+m?2v 又知M:m=4:1 v=
则小物块Q离开平板车时平板车的速度为2v=
(3)、小物块Q在平板车P上滑动的过程中,部分动能转化为内能,由能的转化和守恒定律,知:mgμL=
|

![关于摩擦力,下列说法错误的是[]A.鞋底上的花纹是为了增大鞋底与地面间的摩擦力B.钢丝钳的钳口做得较粗糙是为了增大摩擦力C.缝衣针的表面做得很光滑是为了减少摩擦力D.矿泉水](http://www.00-edu.com/d/file/2022-09-19/b92730bf70e1ef42b5839d473bb1ef18.gif)
![如图所示,物体甲从高H处以速度v1平抛,同时物体乙从距甲水平方向距离x处由地面以速度v2竖直上抛,不计空气阻力,两个物体在空中某处相遇,下列叙述中正确的是[]A.从抛出到相](http://www.00-edu.com/d/file/2022-09-19/2a98326c1cf2920e77551f4865c5b9f3.gif)
