如图,离子源A产生的初速为零、带电量均为e、质量不同的正离子被电压为U0的加速电场加速后匀速通过准直管,垂直射入匀强偏转电场,偏转后通过极板HM上的小孔S离开电场,经过
◎ 题目
| 如图,离子源A产生的初速为零、带电量均为e、质量不同的正离子被电压为U0的加速电场加速后匀速通过准直管,垂直射入匀强偏转电场,偏转后通过极板HM上的小孔S离开电场,经过一段匀速直线运动,垂直于边界MN进入磁感应强度为B的匀强磁场.已知HO=d,HS=2d,∠MNQ=90°.(忽略粒子所受重力) (1)求偏转电场场强E0的大小以及HM与MN的夹角φ; (2)求质量为m的离子在磁场中做圆周运动的半径; (3)若质量为4m的离子垂直打在NQ的中点S1处,质量为16m的离子打在S2处.求S1和S2之间的距离以及能打在NQ上的正离子的质量范围. 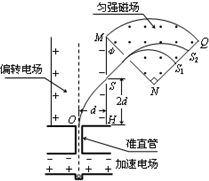 |
◎ 答案
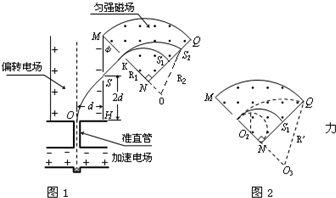 (1)正离子被电压为U0的加速电场加速后速度设为V1,则 对正离子,应用动能定理有eU0=
正离子垂直射入匀强偏转电场,作类平抛运动 受到电场力F=qE0、产生的加速度为a=
垂直电场方向匀速运动,有2d=V1t, 沿场强方向:Y=
联立解得E0=
又tanφ=
(2)正离子进入磁场时的速度大小为V2, 解得V2=
正离子在匀强磁场中作匀速圆周运动,由洛仑兹力提供向心力,qV2B=
解得离子在磁场中做圆周运动的半径R=2
(3)根据R=2
质量为4m的离子在磁场中的运动打在S1,运动半径为R1=2 |

![关于摩擦力,下列说法错误的是[]A.鞋底上的花纹是为了增大鞋底与地面间的摩擦力B.钢丝钳的钳口做得较粗糙是为了增大摩擦力C.缝衣针的表面做得很光滑是为了减少摩擦力D.矿泉水](http://www.00-edu.com/d/file/2022-09-19/b92730bf70e1ef42b5839d473bb1ef18.gif)
![如图所示,物体甲从高H处以速度v1平抛,同时物体乙从距甲水平方向距离x处由地面以速度v2竖直上抛,不计空气阻力,两个物体在空中某处相遇,下列叙述中正确的是[]A.从抛出到相](http://www.00-edu.com/d/file/2022-09-19/2a98326c1cf2920e77551f4865c5b9f3.gif)
