在投掷标枪的比赛中,运动员先要助跑一段距离,借助助跑速度投出标枪,技术动作比较复杂.为了研究最佳助跑距离,将这一过程简化为下面的理想模型:假定运动员先做匀加速运动,
◎ 题目
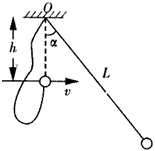
| 在投掷标枪的比赛中,运动员先要助跑一段距离,借助助跑速度投出标枪,技术动作比较复杂.为了研究最佳助跑距离,将这一过程简化为下面的理想模型:假定运动员先做匀加速运动,加速度为a1,投出标枪后立即做匀减速运动,加速度大小为a2,到投掷线时恰好停下.投掷动作瞬间完成,标枪水平投出,看成平抛运动,标枪相对运动员的出手速度是v0,标枪出手高度为h,重力加速度为g.按照上面建立的理想模型,探究下面问题: (1)助跑过程中加速阶段与减速阶段距离之比. (2)在上述条件一定的情况下,为了取得更好成绩,起跑点到投掷线的最佳距离. |
◎ 答案
(1)加速阶段的位移x1=
故助跑过程中加速阶段与减速阶段距离之比a2:a1. (2)设运动员的最大速度v,标枪平抛运动的时间为t,则运动员匀减速运动的位移为:
标枪的有效距离:x=(v+v0)t-
当v=a2t时,x有最大值. 标枪做平抛运动,h=
所以匀加速运动的位移x1=
s=x1+x2= |

![关于摩擦力,下列说法错误的是[]A.鞋底上的花纹是为了增大鞋底与地面间的摩擦力B.钢丝钳的钳口做得较粗糙是为了增大摩擦力C.缝衣针的表面做得很光滑是为了减少摩擦力D.矿泉水](http://www.00-edu.com/d/file/2022-09-19/b92730bf70e1ef42b5839d473bb1ef18.gif)
![如图所示,物体甲从高H处以速度v1平抛,同时物体乙从距甲水平方向距离x处由地面以速度v2竖直上抛,不计空气阻力,两个物体在空中某处相遇,下列叙述中正确的是[]A.从抛出到相](http://www.00-edu.com/d/file/2022-09-19/2a98326c1cf2920e77551f4865c5b9f3.gif)
