濮樺瓨妲搁惇鍏煎皾濡亷绱濈仦杈ㄦЦ閻鍢查懕姘モ偓鍌涱儘闂傤喛顢戞禍鍝勫箵闁綀绔熼敍鐔烘箒閻偐娉╅惄鍫濐槱閵嗗倹澧犳慨瀣偓浣规К瑜版帪绱濋崣鍫モ偓浣告偘瑜版帒骞撻妴鍌濆閸掔増鐫欓崡妤勫垁娑撳﹥妲敍灞藉磮娑撳洤鎷伴弰銉ょ秶閵嗭拷
设质量相等的甲．乙两颗卫星，分别贴近某星球表面和地球表面，环绕其球心做匀速圆周运动，已知该星球和地球的密度比为1：2，其半径分别为R和r，则（1）甲．乙两颗卫星的加速度之比
◎ 题目
| 设质量相等的甲．乙两颗卫星，分别贴近某星球表面和地球表面，环绕其球心做匀速圆周运动，已知该星球和地球的密度比为1：2，其半径分别为R和r，则（1）甲．乙两颗卫星的加速度之比为______；（2）甲．乙两颗卫星所受的向心力之比为______；（3）甲．乙两颗卫星的线速度之比为______；（4）甲．乙两颗卫星的周期之比为______． |
◎ 答案
（1）根据万有引力提供向心力得：
a=
已知该星球和地球的密度比为1：2，其半径分别为R和r， 所以甲．乙两颗卫星的加速度之比为
（2）根据牛顿第二定律得： F向=ma 甲．乙两颗卫星的加速度之比为
所以甲．乙两颗卫星所受的向心力之比为
（3）根据万有引力提供向心力得：
v=
已知该星球和地球的密度比为1：2，其半径分别为R和r， 所以甲．乙两颗卫星的线速度之比为
（4）根据圆周运动公式得： T=鐡掑懎绔舵笟鍨焺鎼存ぞ绗呴崡鏇氱喘閹拷 濮ｅ繐銇夋０鍡楀絿閸掝偊鏁婃潻鍥风礉閸楁洖宕熸导妯诲劕娴滎偂绗夐崑锟�
上一篇：如图所示，质量相等的A、B两物块放在匀速转动的水平圆盘上，随圆盘一起做匀速圆周运动，则下列关系中正确的是（）A．它们所受的摩擦力fA＞fBB．它们的线速度vA＜vBC．它们的运动周期
下一篇：在如图所示的皮带传动装置中，a是大轮边缘上的一点，b是小轮边缘上的一点．当皮带轮匀速转动时，皮带与轮间不打滑，a、b两点的线速度的大小是va______vb；a、b两点的角速度大
零零教育社区：论坛热帖子
|
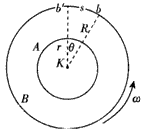
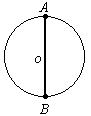
![如图所示，有一皮带传动装置，A、B、C三点到各自转轴的距离分别为RA、RB、RC，已知RB=RC=RA/2，若在传动过程中，皮带不打滑。则[]A、A点与C点的角速度大小相等B、A点与C点的](http://www.00-edu.com/d/file/2022-09-22/4f3c88b50c2fa903804d354d5b1fdc83.png)
