如图所示,把中心带有小孔的平行放置的两个圆形金属板M和N,连接在电压恒为U的直流电源上.一个质量为m,电荷量为q的微观正粒子,以近似于静止的状态,从M板中心的小孔进入电
◎ 题目
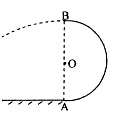
| 如图所示,把中心带有小孔的平行放置的两个圆形金属板M和 N,连接在电压恒为U的直流电源上.一个质量为m,电荷量为q的微观正粒子,以近似于静止的状态,从M板中心的小孔进入电场,然后又从N板中心的小孔穿出,再进入磁感应强度为B的足够宽广的匀强磁场做中运动. 那么: (1)该粒子从N板中心的小孔穿出时的速度有多大? (2)该粒子在磁场中受到的洛仑兹力是多大? (3)若圆形板N的半径为R,如果该粒子返回后能够直接打在圆形板N的右侧表面上,那么该磁场的磁感应强度B至少为多大?  |
◎ 答案
(1)粒子进入电场的过程,根据动能定理有:qU=
所以粒子穿出小孔时的速度大小为: v=
(2)粒子在磁场中受到的洛仑兹力大小:f=qvB=qB
(3)粒子进入磁场做匀速圆周运动,洛伦兹力提供向心力:qvB=m
解得r=
所以粒子的圆轨道半径:r=
那么,粒子打在N板上的条件是:R≥2r=2
所以,粒子能够要在N板上,要求B至少为: B=2
|

![一辆卡车在丘陵地匀速行驶,地形如图所示,由于轮胎太旧,途中爆胎,爆胎可能性最大的地段应是[]A、a处B、b处C、c处D、d处](http://www.00-edu.com/d/file/2022-09-29/9361808a019cadbd3e04461b0d6b4b2d.gif)

![如图,小明看到鸡蛋浮在盐水面上,他沿杯壁缓慢加入清水使鸡蛋下沉。在此过程中,鸡蛋受到的浮力F随时间t的变化图像可能是下图中的[]A.B.C.D.](http://www.00-edu.com/d/file/2022-09-29/670cdea52633e427344305a04e5cce7a.gif)
![如图所示,小球在竖直放置的光滑圆形管道内做圆周运动,内侧壁半径为R,小球半径为r(略小于管道口径),则下列说法正确的是[]A.小球通过最高点时的最小速度B.小球通过最高点时](http://www.00-edu.com/d/file/2022-09-29/75d38327ba18f2798edb1e4da873479c.gif)
