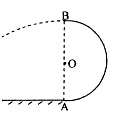
如图所示半径为R、r(R>r)甲、乙两圆形轨道安置在同一竖直平面内,两轨道之间由一条水平轨道(CD)相连,如小球从离地3R的高处A点由静止释放,可以滑过甲轨道,经过CD段又滑上乙
◎ 题目
| 如图所示半径为R、r(R>r)甲、乙两圆形轨道安置在同一竖直平面内,两轨道之间由一条水平轨道(CD)相连,如小球从离地3R的高处A点由静止释放,可以滑过甲轨道,经过CD段又滑上乙轨道后离开两圆形轨道,小球与CD段间的动摩擦因数为μ,其余各段均光滑. (1)求小球经过甲圆形轨道的最高点时小球的速度? (2)为避免出现小球脱离圆形轨道而发生撞轨现象.试设计CD段的长度.  |
◎ 答案
| (1)设小球能通过甲轨道最高点时速度为v1. 由机械能守恒定律得:mgh=mg.2R+
解得v1=
故小球经过甲圆形轨道的最高点时的速度为
(2)小球在甲轨道上做圆周运动通过最高点的最小速度为 vmin=
∵v1=
设CD的长度为x,小球在乙轨道最高点的最小速度为v2=
小球要通过乙轨道最高点,根据动能定理得:mg(3R-2r)-μmgx=
所以x≤
小球到乙轨圆心等高处之前再返回,根据动能定理得:mg(3R-r)-μmgx=0 解得:x=
小球到乙轨的最低点速度恰好速度为0,根据动能定理得:mg3R-μmgx=0 解得:x=
所以 |

![一辆卡车在丘陵地匀速行驶,地形如图所示,由于轮胎太旧,途中爆胎,爆胎可能性最大的地段应是[]A、a处B、b处C、c处D、d处](http://www.00-edu.com/d/file/2022-09-29/9361808a019cadbd3e04461b0d6b4b2d.gif)

![如图,小明看到鸡蛋浮在盐水面上,他沿杯壁缓慢加入清水使鸡蛋下沉。在此过程中,鸡蛋受到的浮力F随时间t的变化图像可能是下图中的[]A.B.C.D.](http://www.00-edu.com/d/file/2022-09-29/670cdea52633e427344305a04e5cce7a.gif)
![如图所示,小球在竖直放置的光滑圆形管道内做圆周运动,内侧壁半径为R,小球半径为r(略小于管道口径),则下列说法正确的是[]A.小球通过最高点时的最小速度B.小球通过最高点时](http://www.00-edu.com/d/file/2022-09-29/75d38327ba18f2798edb1e4da873479c.gif)
