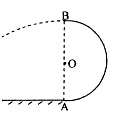
如图所示，AB段为一半径R=0.2m的光滑14圆弧轨道，EF为一倾角是30°的足够长的光滑固定斜面，斜而上有一质量为0.1kg的薄木板CD，开始时薄木板被锁定．一质量也为0.1kg的物块
◎ 题目
如图所示，AB段为一半径R=0.2m的光滑
（1）物块到达B点时对圆弧轨道的压力； （2）物块滑上薄木板时的速度大小； （3）达到共同速度前物块下滑的加速度大小及从物块滑上薄木板至达到共同速度所用的时间．  |
◎ 答案
| （1）物块从A到B过程，只有重力做功，根据机械能守恒定律得 mgR=
解得，vB=
在B点，由牛顿第二定律得： N-mg=m
解得，N=3N 根据牛顿第三定律得：物块到达B点时对圆弧轨道的压力大小为3N，方向竖直向下． （2）设物块到达斜面上的速度为v，则由题意得 cos30°=
解得，v=
（3）在物块滑上薄木板的过程中，由牛顿第二定律得 对物块：mgsin30°-μmgcos30°=ma1 解得，a1=2.5m/s2 对木板：mgsin30°+μmgcos30°=ma2 解得，a2=7.5m/s2 设从物块滑上薄木板至达到共同速度所用的时间为t，则有 v+a1t=a2t 解得，t=
答： （1）物块到达B点时对圆弧轨道的压力是2m/s； （2）物块滑上薄木板时的速度大小是 |
![一辆卡车在丘陵地匀速行驶，地形如图所示，由于轮胎太旧，途中爆胎，爆胎可能性最大的地段应是[]A、a处B、b处C、c处D、d处](http://www.00-edu.com/d/file/2022-09-29/9361808a019cadbd3e04461b0d6b4b2d.gif)
![如图，小明看到鸡蛋浮在盐水面上，他沿杯壁缓慢加入清水使鸡蛋下沉。在此过程中，鸡蛋受到的浮力F随时间t的变化图像可能是下图中的[]A.B.C.D.](http://www.00-edu.com/d/file/2022-09-29/670cdea52633e427344305a04e5cce7a.gif)
![如图所示，小球在竖直放置的光滑圆形管道内做圆周运动，内侧壁半径为R，小球半径为r（略小于管道口径），则下列说法正确的是[]A．小球通过最高点时的最小速度B．小球通过最高点时](http://www.00-edu.com/d/file/2022-09-29/75d38327ba18f2798edb1e4da873479c.gif)
