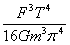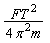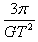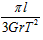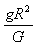宇航员站在一星球表面上的某高处,沿水平方向抛出一小球.经过时间t,小球落到星球表面,测得抛出点与落地点之间的距离为L。若抛出时的初速度增大到原来的2倍,则抛出点与落地
◎ 题目
宇航员站在一星球表面上的某高处,沿水平方向抛出一小球.经过时间t,小球落到星球表面,测得抛出点与落地点之间的距离为L。若抛出时的初速度增大到原来的2倍,则抛出点与落地点之间的距离为 L。已知两落地点在同一水平面上,该星球的半径为R,引力常量为G。求该星球的质量M。 L。已知两落地点在同一水平面上,该星球的半径为R,引力常量为G。求该星球的质量M。 |
◎ 答案
解:如图所示,设抛出点的高度为h,第一次时平抛的水平射程为x,则有x2+h2=L2 ① 由平抛运动的规律可知,当抛出的初速度增大到原来的2倍时,其水平射程应增大到2x,可得(2x)2+h2=(  L)2 ② L)2 ②由①②解得:h=  L L设该星球表面的重力加速度为g,由平抛规律可得h=  gt2 ③ gt2 ③又因为  =mg ④ =mg ④由③④得M=  |
◎ 解析
“略”◎ 知识点
专家分析,试题“宇航员站在一星球表面上的某高处,沿水平方向抛出一小球.经过时间t,小球落到星球表面,测得抛出点与落地点之间的距离为L。若抛出时的初速度增大到原来的2倍,则抛出点与落地…”主要考查了你对 【平抛运动】,【计算天体质量与密度】 等知识点的理解和应用能力。关于这些知识点的“档案”,你可以点击相应的链接进行查看和学习。- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
上一篇:2009年7月22日我国发生了近60年来最大规模的一次日全食,如图所示是某兴趣小组在该次观测活动中拍摄的太阳刚好被全部遮住时的照片。该兴趣小组查阅资料得知地球直径为1.3×1
下一篇:天宫一号于2011年9月29日21时16分3秒在酒泉卫星发射中心发射,设计在轨寿命两年。在轨运动可近似看做匀速圆周运动,已知它的轨道半径为r,运行周期为T,万有引力恒量为G,则
零零教育社区:论坛热帖子
| [高考] 2022 西安电子科技大学《软件工程》大作业答案 (2022-04-25) |
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |