人造地球卫星绕地球旋转时,既具有动能又具有引力势能(引力势能实际上是卫星与地球共有的,简略地说此势能是人造卫星所具有的).设地球的质量为M,以卫星离地无限远处时的引力
◎ 题目
人造地球卫星绕地球旋转时,既具有动能又具有引力势能(引力势能实际上是卫星与地球共有的,简略地说此势能是人造卫星所具有的).设地球的质量为M,以卫星离地无限远处时的引力势能为零,则质量为m的人造卫星在距离地心为r处时的引力势能为Ep=-
(1)试证明:在大气层外任一轨道上绕地球做匀速圆周运动的人造卫星所具有的机械能的绝对值恰好等于其动能. (2)当物体在地球表面的速度等于或大于某一速度时,物体就可以挣脱地球引力的束缚,成为绕太阳运动的人造卫星,这个速度叫做第二宇宙速度,用v2表示.用R表示地球的半径,M表示地球的质量,G表示万有引力常量.试写出第二宇宙速度的表达式. (3)设第一宇宙速度为v1,证明:v2=
|
◎ 答案
(1)设卫星在半径为r的轨道上做匀速圆周运动的速度为v,地球的质量为M,卫星的质量为m.有万有引力提供卫星做圆周运动的向心力:G
所以,人造卫星的动能:Ek=
卫星在轨道上具有的引力势能为:Ep=-
所以卫星具有的引力势能为:E=Ek+Ep=
所以:|E|=|-
(2)设物体在地于表面的速度为v2,当它脱离地球引力时r→∞,此时速度为零,由机械能守恒定律得:
|

![某人造卫星绕地球做匀速圆周运动,设地球半径为R,地面重力加速度为g,下列说法正确的是[]A.人造卫星的最小周期为2πB.卫星在距地面高度为R处的绕行速度为C.卫星在距地面高度](http://www.00-edu.com/d/file/2022-10-05/72f1da21381abd63d66a2371ad24123c.gif)
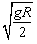
![如图所示,a、b、c是在地球大气层外圆形轨道上运行的三颗人造卫星。下列说法中正确的是[]A.b、c的线速度大小相等,且大于a的线速度B.b、c的向心加速度大小相等,且小于a的](http://www.00-edu.com/d/file/2022-10-05/a8f48d42451f411778000fa3222321fe.gif)
