A、B两行星在同一平面内绕同一恒星做匀速圆周运动,运行方向相同,A的轨道半径为rl,B的轨道半径为r2.已知恒星质量为M,恒星对行星的引力远大于行星间的引力,两行星的轨道半
◎ 题目
| A、B两行星在同一平面内绕同一恒星做匀速圆周运动,运行方向相同,A的轨道半径为rl,B的轨道半径为r2.已知恒星质量为M,恒星对行星的引力远大于行星间的引力,两行星的轨道半径r1<r2.若在某时刻两行星相距最近,试求: (1)再经过多少时间两行星距离又最近? (2)再经过多少时间两行星距离又最远? |
◎ 答案
| (1)A、B两行星距离最近时A、B与恒星在同一条圆半径上. A、B运动方向相同,A更靠近恒星,A的转动角速度大、周期短.如果经过时间t,A、B与恒星连线半径转过的角度相差2π的整数倍,则A、B与恒星又位于同一条圆半径上,距离最近. 设A、B的角速度分别为ω1,ω2,经过时间t,A转过的角速度为ω1t,B转过的角度为ω2t.A、B距离最近的条件是:ω1t-ω2t=n×2π(n=1,2,3…) 恒星对行星的引力提供向心力,则:
由此得出:ω1=
求得:t=
(2)如果经过时间tˊ,A、B转过的角度相差π的奇数倍时,则A、B相距最远, 即:ω1t′-ω2t'=(2k-1)π(k=1,2,3…),得:t′= |

![某人造卫星绕地球做匀速圆周运动,设地球半径为R,地面重力加速度为g,下列说法正确的是[]A.人造卫星的最小周期为2πB.卫星在距地面高度为R处的绕行速度为C.卫星在距地面高度](http://www.00-edu.com/d/file/2022-10-05/72f1da21381abd63d66a2371ad24123c.gif)
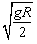
![如图所示,a、b、c是在地球大气层外圆形轨道上运行的三颗人造卫星。下列说法中正确的是[]A.b、c的线速度大小相等,且大于a的线速度B.b、c的向心加速度大小相等,且小于a的](http://www.00-edu.com/d/file/2022-10-05/a8f48d42451f411778000fa3222321fe.gif)
