某宇航员在飞船发射前测得自身连同宇航服等随身装备共重840N,在火箭发射阶段,发现当飞船随火箭以a=g/2的加速度匀加速竖直上升到某位置时(其中g为地球表面处的重力加速度),
◎ 题目
某宇航员在飞船发射前测得自身连同宇航服等随身装备共重840N,在火箭发射阶段,发现当飞船随火箭以a=g/2的加速度匀加速竖直上升到某位置时(其中g为地球表面处的重力加速度),其身下体重测试仪的示数为1220N.设地球半径R=6400km,地球表面重力加速度g=10m/s2(求解过程中可能用到
(1)该位置处的重力加速度g′是地面处重力加速度g的多少倍? (2)该位置距地球表面的高度h为多大? |
◎ 答案
(1)对宇航员受力分析如图: 设:该位置处的重力加速度g′,由牛顿第二定律得: FN-mg′=m?
即:1220-84g′=84?
解得:g′=
(2)设此处距地面高度为h,地球质量为M,半径为R; 物体在地面时:
物体在高为h处时:
两式联立得:
解得:h=
答:(1)该位置处的重力加速度g′是地面处重力加速度g的
(2)该位置距地球表面的高度h为128km. |
◎ 解析
“略”- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
上一篇:1998年1月发射的“月球勘探号”空间探测器动用最新科技手段对月球进行近距离环绕勘探,探测到月球不同区域密度不同.当探测器飞越密度较小地区时,通过地面大口径射电望远镜观察
下一篇:质量相等的两个球,分别在地球表面和月球表面以相等的初速率竖直上抛,若不计空气阻力,则()A.上升到最高点的过程中,它们受到的重力冲量大小相等B.上升到最高点的过程中,它
零零教育社区:论坛热帖子
| [高考] 2022 西安电子科技大学《软件工程》大作业答案 (2022-04-25) |
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |

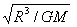
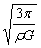
![地球半径为R,地球表面的重力加速度为g,若高空中某处的重力加速度为g/2,则该处距地面球表面的高度为[]A.(-1)RB.RC.RD.2R](http://www.00-edu.com/d/file/2022-10-06/5e45b1bcec1b2ecd1bba3e87155ff50d.gif)
![如图所示,有A、B两个行星绕同一恒星O沿不同轨道做匀速圆周运动,旋转方向相同。A行星的周期为,B行星的周期为,在某一时刻两行星第一次相遇(即两行星距离最近),则[]A.经过](http://www.00-edu.com/d/file/2022-10-06/78b505558d79326551557f3ea62cf016.gif)
