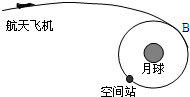
两个靠得很近的天体,离其它天体非常遥远,它们以其连线上某一点O为圆心各自做匀速圆周运动,两者的距离保持不变,科学家把这样的两个天体称为“双星”,如图所示.已知双星的质
◎ 题目
两个靠得很近的天体,离其它天体非常遥远,它们以其连线上某一点O为圆心各自做匀速圆周运动,两者的距离保持不变,科学家把这样的两个天体称为“双星”,如图所示.已知双星的质量为m1和m2,它们之间的距离为L.求双星运行轨道半径r1和r2,以及运行的周期T. |
◎ 答案
 如图, 设双星中质量为m1的天体轨道半径为r1,质量为m1的天体轨道半径为r2 据万有引力定律和牛顿第二定律,得: G
G
r1+r2=L③ 由①②③联立解得: r1=
r2=
再由:G
运行的周期T=2πL
答:双星运行轨道半径分别为:r1=
|

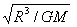
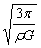
![地球半径为R,地球表面的重力加速度为g,若高空中某处的重力加速度为g/2,则该处距地面球表面的高度为[]A.(-1)RB.RC.RD.2R](http://www.00-edu.com/d/file/2022-10-06/5e45b1bcec1b2ecd1bba3e87155ff50d.gif)
