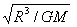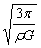如图所示为宇宙中一个恒星系的示意图,其中A为该星系中的一颗行星,它绕中央恒星O运行的轨道近似为圆.天文学家观测得到A行星运行的轨道半径为r,周期为T.已知万有引力常量G.
◎ 题目
| 如图所示为宇宙中一个恒星系的示意图,其中A为该星系中的一颗行星,它绕中央恒星O运行的轨道近似为圆.天文学家观测得到A行星运行的轨道半径为r,周期为T.已知万有引力常量G. (1)求A行星做匀速圆周运动的向心加速度大小; (2)求中央恒星O的质量; (3)若中央恒星是半径为R的均匀球体,要使在此恒星表面被平抛出的物体不再落回恒星表面,通过计算说明抛出物体的速度需要满足什么条件.  |
◎ 答案
| (1)根据圆周运动的向心加速度的表达式得出: A行星绕恒星做匀速圆周运动的加速度大小为:a=ω2r=
(2)A行星绕恒星O做匀速圆周运动,设A行星和恒星的质量分别为m和M,根据万有引力定律和牛顿第二定律有:G
解得:M=
(3)当水平抛出物体的速度大小等于或大于物体在靠近恒星表面,绕恒星做匀速圆周运动速度大小时,物体将不再落回恒星表面.设物体在靠近恒星表面,绕恒星做半径为R的匀速圆周运动的速度大小为υ,也就是我们所说的第一宇宙速度,根据万有引力定律和牛顿第二定律有:G
代入M解得:v=
即在恒星表面水平抛出物体,物体不再落回恒星表面,抛出物体的速度v'需满足的条件是:v′≥
|