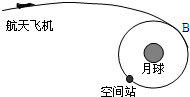
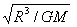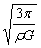图示为宇宙中一恒星系的示意图,A为该星系的一颗行星,它绕中央恒星O的运行轨道近似为圆.已知引力常量为G,天文学家观测得到A行星的运行轨道半径为R0,周期为T0(1)中央恒星O
◎ 题目
| 图示为宇宙中一恒星系的示意图,A为该星系的一颗行星,它绕中央恒星O的运行轨道近似为圆.已知引力常量为G,天文学家观测得到A行星的运行轨道半径为R0,周期为T0 (1)中央恒星O的质量是多大? (2)长期观测发现A行星每隔t0时间其运行轨道便会偏离理论轨道少许,天文学家认为出现这种现象的原因可能是A行星外侧还存在着一颗未知的行星B(假设其运行的圆轨道与A在同一平面内,且与A的绕行方向相同).根据上述现象和假设,试估箅未知行星B的运动周期和轨道半径.  |
◎ 答案
| (1)设中央恒星质量为M,A行星质量为m, 由万有引力提供向心力得:G
解得:M=
故中央恒星O的质量为
(2)由题意可知:A、B相距最近时,B对A的影响最大,且每隔时间t0发生一次最大的偏离,说明A、B相距最近,设B行星的周期为T,则有: (
解得:T=
据开普勒第三定律:
得:R= |