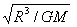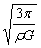水是眼波横,山是眉峰聚。欲问行人去那边?眉眼盈盈处。才始送春归,又送君归去。若到江南赶上春,千万和春住。
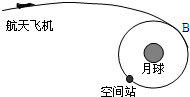
假定地球、月球都静止不动,用火箭从地球沿地月连线发射一探测器.假定探测器在地球表面附近脱离火箭.用W表示探测器从脱离火箭处飞到月球的过程中克服地球引力做的功,用Ek表

◎ 题目
假定地球、月球都静止不动,用火箭从地球沿地月连线发射一探测器.假定探测器在地球表面附近脱离火箭.用W表示探测器从脱离火箭处飞到月球的过程中克服地球引力做的功,用Ek表示探测器脱离火箭时的动能,若不计空气阻力,则( )
|
◎ 答案
| 探测器脱离火箭后同时受到地球的引力和月球的引力, 根据F=G
可知开始时物体受到地球的引力大于受到月球的引力,后来受到月球的引力大于受到地球的引力, 所以探测器在运动的过程中地球的引力对物体做负功,月球的引力对物体做正功, 所以探测器能够到达月球的条件是必须克服地球引力做功越过引力相等的位置. 又根据F=G
设在探测器运动的过程中月球引力对探测器做的功为W1,探测器克服地球引力对探测器做的功为W,并且W1<W, 若探测器恰好到达月球,则根据动能定理可得 -W+W1=EK末-Ek, 即EK末=EK-W+W1 故探测器能够到达月球的条件是Ek末=EK-W+W1≥0, 即EK≥W-W1, 故EK小于W时探测器也可能到达月球. 故B正确. 由于M地≈81M月, 故W≈81W1 假设当EK=
相矛盾,故假设不正确.即探测器一定不能到达月球. 故D正确. 故选B、D. |
◎ 解析
“略”◎ 知识点
专家分析,试题“假定地球、月球都静止不动,用火箭从地球沿地月连线发射一探测器.假定探测器在地球表面附近脱离火箭.用W表示探测器从脱离火箭处飞到月球的过程中克服地球引力做的功,用Ek表…”主要考查了你对 【万有引力定律的其他应用】,【动能定理】 等知识点的理解和应用能力。关于这些知识点的“档案”,你可以点击相应的链接进行查看和学习。 超市便利店下单优惠 每天领取别错过,单单优惠享不停- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
上一篇:如图所示,飞船在绕地球无动力飞行过程中沿如图所示椭圆轨道运行,地球的中心位于椭圆的-个焦点上.A为椭圆轨道的近地点,B为椭圆轨道的远地点.则飞船从A点开始沿椭圆轨道运行
下一篇:如图所示,发射地球同步卫星时,可认为先将卫星发射至距地面高度为h1的圆形近地轨道上,在卫星经过A点时点火(喷气发动机工作)实施变轨进入椭圆轨道,椭圆轨道的近地点为A,远
零零教育社区:论坛热帖子
| [高考] 2022 西安电子科技大学《软件工程》大作业答案 (2022-04-25) |
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |