如图所示,光滑绝缘水平桌面上固定一绝缘挡板P,质量分别为mA和mB的小物块A和B(可视为质点)分别带有+QA和+QB的电荷量,两物块由绝缘的轻弹簧相连,一不可伸长的轻绳跨过定滑
◎ 题目
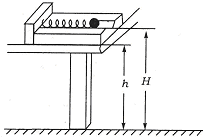
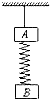
| 如图所示,光滑绝缘水平桌面上固定一绝缘挡板P,质量分别为mA和mB的小物块A和B(可视为质点)分别带有+QA和+QB的电荷量,两物块由绝缘的轻弹簧相连,一不可伸长的轻绳跨过定滑轮,一端与物块B连接,另一端连接轻质小钩.整个装置处于正交的场强大小为E、方向水平向左的匀强电场和磁感应强度大小为B、方向水平向里的匀强磁场中.物块A,B开始时均静止,已知弹簧的劲度系数为K,不计一切摩擦及AB间的库仑力,物块A、B所带的电荷量不变,B不会碰到滑轮,物块A、B均不离开水平桌面.若在小钩上挂一质量为M的物块C并由静止释放,可使物块A对挡板P的压力为零,但不会离开P,则 (1)求物块C下落的最大距离; (2)求小物块C下落到最低点的过程中,小物块B的电势能的变化量、弹簧的弹性势能变化量; (3)若C的质量改为2M,求小物块A刚离开挡板P时小物块B的速度大小以及此时小物块B对水平桌面的压力.  |
◎ 答案
| (1)开始时弹簧的形变量为x1, 对物体B由平衡条件可得:kx1=QBE 设A刚离开挡板时, 弹簧的形变量为x2, 对物块B由平衡条件可得:kx2=QAE 故C下降的最大距离为:h=x1+x2=
(2)物块C由静止释放下落h至最低点的过程中, B的电势能增加量为: △Ep=QBEh=
由能量守恒定律可知: 物块由静止释放至下落h至最低点的过程中, c的重力势能减小量等于 B的电势能的增量和弹簧弹性势能的增量 即:Mgh=QBEh+△E弹 解得:△E弹=
故小物块C下落到最低点的过程中,小物块B的电势能的变化量为
(3)当C的质量为2M时, 设A刚离开挡板时B的速度为V, 由能量守恒定律可知:2Mgh=QBEh+△E弹+
解得A刚离开P时B的速度为:V=
因为物块AB均不离开水平桌面, 设物体B所受支持力为NB1,所以对物块B竖直方向受力平衡: mBg=NB1+QBvB 由牛顿第三定律得:NB=NB1 解得:NB=mBg-BQB |

![如图所示的四种现象中,由于光的直线传播形成的是[]A.B.C.D.](http://www.00-edu.com/d/file/2022-10-16/d78c8212763d7a2e0d4cf9580ff50227.gif)