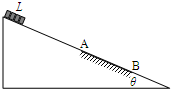
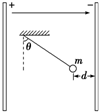
如图所示,一个半径为R的半球形的碗固定在桌面上,碗口水平,O点为其球心,碗的内表面及碗口是光滑的.一根轻质细线跨在碗口上,线的两端分别系有小球A和B,当它们处于平衡状
◎ 题目
| 如图所示,一个半径为R的半球形的碗固定在桌面上,碗口水平,O点为其球心,碗的内表面及碗口是光滑的.一根轻质细线跨在碗口上,线的两端分别系有小球A和B,当它们处于平衡状态时,小球A与O点的连线与水平线的夹角为60°. (1)求小球A与小球B的质量比mA:mB; (2)现将A球质量改为2m、B球质量改为m,且开始时A球位于碗口C点,由静止沿碗下滑,当A球滑到碗底时,求两球总的重力势能改变量; (3)在(2)条件下,当A球滑到碗底时,求B球的速度大小.  |
◎ 答案
| (1)设绳的张力为T.对A球进行受力分析,有 Nsin60°+Tsin60°=mAg Ncos60°=Tcos60° 对B球进行受力分析,有T=mBg 可解得:mA:mB=
(2)A球的重力势能改变量为△EpA=-mAgR=-2mgR B两球的重力势能改变量为△EpB=mBg?
所以A、B两球总的重力势能改变量为△Ep=△EpA+△EpB=-(2-
负号表示两球的重力势能减少. (3)当A球滑到碗底时,设A、B两球的速度分别为vA、vB,则vAcos45°=vB(1) 根据A、B两球总机械能守恒,有△EK+△Ep=0(2) 即
联立以上三式,解得:vB= |