如图所示,电源电动势为ε,内阻为r,滑动变阻器总阻值为3r,间距为d的两平行金属板AB、CD竖直放置,闭合电键S时,板间电场可视为匀强电场.板间有一长为L的绝缘细轻杆,能绕水
◎ 题目
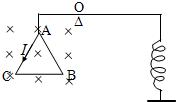
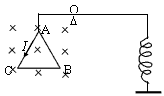
如图所示,电源电动势为ε,内阻为r,滑动变阻器总阻值为3r,间距为d的两平行金属板AB、CD竖直放置,闭合电键S时,板间电场可视为匀强电场.板间有一长为L的绝缘细轻杆,能绕水平固定转轴O在竖直面内无摩擦转动,杆上端固定质量为m、带电量为+q的金属小球a,下端固定质量为2m、带电量为-q的金属小球b,已知Ob=2Oa,并且q=
(1)求两极板间电场强度E的表达式; (2)将轻杆从如图位置顺时针转过θ时(θ<360°)由静止释放,轻杆恰能静止,求θ; (3)若将轻杆从如图位置由静止释放,轻杆将绕轴O顺时针转动,求小球a运动的最大速度. 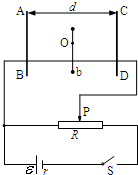 |
◎ 答案
 (1)由题意可知,当滑动变阻器滑片位于变阻器中点时,闭合电键S,平行金属板间的电压 U=
U=
又因为平行金属板间是匀强电场,根据电场强度与电势差的关系有: E=
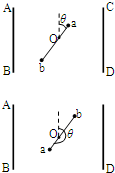
(2)轻杆恰能静止时所受力矩平衡, 两小球所受重力的力矩为反方向,且M重a<M重b 两小球所受电场力的力矩为同方向, 因此力矩平衡时则有:M重a+M电a+M电b=M重b mgsinθ×
又因为Eq=
可解得θ=37°或217° (3)由(2)分析知小球P运动的速度最大时轻杆与竖直方向夹角为37°,因为同杆转动,所以有: vb=2va 由动能定理得:
可解出va= |