水是眼波横,山是眉峰聚。欲问行人去那边?眉眼盈盈处。才始送春归,又送君归去。若到江南赶上春,千万和春住。
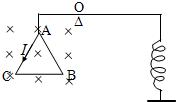
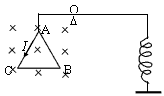
如图所示,两个带电小球(可视为质点),固定在轻质绝缘等腰直角三角形框架OAB的两个端点A、B上,整个装置可以绕过O点且垂直于纸面的水平轴在竖直平面内自由转动.直角三角形的

◎ 题目
| 如图所示,两个带电小球(可视为质点),固定在轻质绝缘等腰直角三角形框架OAB的两个端点A、B上,整个装置可以绕过O点且垂直于纸面的水平轴在竖直平面内自由转动.直角三角形的直角边长为L.质量分别为mA=3m,mB=m,电荷量分别为QA=-q,QB=+q.重力加速度为g. (1)若施加竖直向上的匀强电场E,使框架OB边水平、OA边竖直并保持静止状态,则电场强度E多大? (2)若将匀强电场方向改为与原电场方向相反,保持E的大小不变,则框架OAB在接下来的运动过程中,带电小球A的最大动能EkA为多少? (3)在(2)中,设以O点为零势能位,则框架OAB在运动过程中,A、B小球电势能之和的最小值E′为多少? 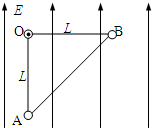 |
◎ 答案
| (1)以O为支点,根据三角架力矩平衡,M顺=M逆 mgL=qEL 求得E=
(2)设OA边与竖直方向成α,当系统的力矩平衡时动能最大,则有 M顺=M逆 即 3mgLsinα=mgLcosα+qELcosα+qELsinα 解得,OA杆与竖直方向夹角α=45°时A球动能最大. 根据系统动能定理W合=△EK,得 -3mgL(1-cos45°)+mgLsin45°+qEL sin45°+qEL(1-cos45°)=
求得A球最大速度v=
得到A球动能EKA=
(3)设OA边与竖直方向成α时系统的速度为零,根据系统动能定理 -3mgL(1-cosα)+mgLsinα+qELsinα+qEL(1-cosα)=0 得α=90°时系统速度为零,不能再继续转过去了. 由于该过程电场力一直做正功,A、B小球电势能之和一直减小,所以此处A、B小球电势能之和最小,E′=-qEL=-mgL. 答: (1)电场强度E是
(2)框架OAB在接下来的运动过程中,带电小球A的最大动能EkA为
(3)框架OAB在运动过程中,A、B小球电势能之和的最小值E′为-mgL. |
◎ 解析
“略”◎ 知识点
专家分析,试题“如图所示,两个带电小球(可视为质点),固定在轻质绝缘等腰直角三角形框架OAB的两个端点A、B上,整个装置可以绕过O点且垂直于纸面的水平轴在竖直平面内自由转动.直角三角形的…”主要考查了你对 【力矩的平衡】,【动能定理】,【电势能】 等知识点的理解和应用能力。关于这些知识点的“档案”,你可以点击相应的链接进行查看和学习。 超市便利店下单优惠 每天领取别错过,单单优惠享不停- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
上一篇:有人设计了一种新型伸缩拉杆秤.结构如图,秤杆的一端固定一配重物并悬一挂钩,秤杆外面套有内外两个套筒,套筒左端开槽使其可以不受秤纽阻碍而移动到挂钩所在的位置(设开槽后
下一篇:如图,质量均为m的两个小球A、B固定在弯成120°角的绝缘轻杆两端,OA和OB的长度均为l,可绕过O点且与纸面垂直的水平轴无摩擦转动,空气阻力不计.设A球带正电,B球带负电,电量
零零教育社区:论坛热帖子
| [高考] 2022 西安电子科技大学《软件工程》大作业答案 (2022-04-25) |
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |