如图所示,绝缘细绳绕过轻滑轮连接着质量为m的正方形导线框和质量为M的物块,导线框的边长为L、电阻为R.物块放在光滑水平面上,线框平面竖直且ab边水平,其下方存在两个匀强
◎ 题目
| 如图所示,绝缘细绳绕过轻滑轮连接着质量为m的正方形导线框和质量为M的物块,导线框的边长为L、电阻为R.物块放在光滑水平面上,线框平面竖直且ab边水平,其下方存在两个匀强磁场区域,磁感应强度的大小均为B,方向水平但相反,Ⅰ区域的高度为L,Ⅱ区域的高度为2L. 开始时,线框ab边距磁场上边界PP′的高度也为L,各段绳都处于伸直状态,把它们由静止释放,运动中线框平面始终与磁场方向垂直,M始终在水平面上运动,当ab边刚穿过两磁场的分界线QQ′进入磁场Ⅱ时,线框做匀速运动,不计滑轮处的摩擦.求: (1)ab边刚进入磁场Ⅰ时,线框的速度大小; (2)cd边从PP′位置运动到QQ′位置过程中,通过线圈导线某横截面的电荷量; (3)ab边从PP′位置运动到NN′位置过程中,线圈中产生的焦耳热. 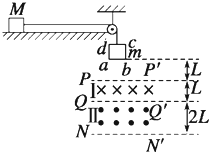 |
◎ 答案
| (1)对线框和物块组成的整体,由机械能守恒定律 mgL=
v1=
(2)线框从Ⅰ区进入Ⅱ区过程中, △Φ=Φ2-Φ1=2BL2 E=
I=
通过线圈导线某截面的电量:q=I△t=
(3)线框ab边运动到位置NN′之前,线框只有ab边从PP′位置下降2L的过程中才有感应电流,设线框ab边刚进入Ⅱ区域做匀速运动的速度是v2,线圈中电流为I2, I2=
此时M、m均做匀速运动,2BI2L=mg v2=
根据能量转化与守恒定律,mg?3L=
则线圈中产生的焦耳热为:Q=3mgL-
答:(1)ab边刚进入磁场Ⅰ时,线框的速度大小是
(2)cd边从PP′位置运动到QQ′位置过程中,通过线圈导线某横截面的电荷量是 |


![一个物体受到一个与它速度方向相同、随时间变化如图所示的力的作用,物体的速度、加速度的变化情况是[]A.加速度逐渐增大,速度逐渐增大B.加速度逐渐增大,速度逐渐减小C.加速](http://www.00-edu.com/d/file/2022-10-29/6e15248d1944417389401f31b9661c0b.gif)