如图所示，光滑水平地面上停着一辆平板车，其质量为2m，长为L，车右端（A点）有一块静止的质量为m的小金属块．金属块与车间有摩擦，以中点C为界，AC段与CB段动摩擦因数不同．现给

首页 > 考试 > 物理 > 高中物理 > 牛顿第二定律/2022-10-29 / 加入收藏 / 阅读 [打印]

◎ 题目

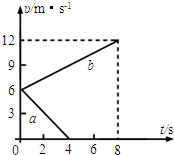
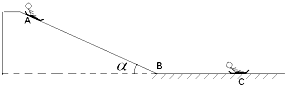
如图所示，光滑水平地面上停着一辆平板车，其质量为2m，长为L，车右端（A点）有一块静止的质量为m的小金属块．金属块与车间有摩擦，以中点C为界，AC段与CB段动摩擦因数不同．现给车施加一个向右的水平恒力，使车向右运动，同时金属块在车上开始滑动，当金属块滑到中点C时，即撤去这个力．已知撤去力的瞬间，金属块的速度为v0，车的速度为2v0，最后金属块恰停在车的左端（B点）．
求：（1）F的大小为多少？
（2）AC段与CB段动摩擦因数μ1与μ2的比值．
魔方格

◎ 答案

（1）设水平拉力为F，力的作用时间为t1，
对金属块，由牛顿第二定律可得：a1=
μ1mg
m
=μ1g，
由匀变速直线运动的速度公式可知，v0=a1t1，则t1=
v0
μ1g
；
对小车，由牛顿第二定律可得：a2=
(F-μ1mg)
2m
，
由匀变速直线运动的速度公式可知：
2v0=a2t1=
(F-μ1mg)
2m
×
v0
μ1g
，则F=5μ1mg  ①；
在A→C过程中，由动能定理得：
对金属块：μ1mgs1=
1
2
mv02 ②，
对小车：（F-μ1mg）s2=
1
2
2m（2v0）2 ③，
由几何关系可知：s2-s1=
L
2
    ④，
由①②③④解得：μ1=
v20
gL
，F=
5m
v20
L
；
（2）从小金属块滑至车中点C开始到小金属块停在车的左端的过程中，
系统外力为零，动量守恒，设共同速度为v，由2m×2v0+mv0=（2m+m）v，得v=
5
3
v0，
由能量守恒得：μ2mg
L
2
=
1
2
mv02+
1
2
×2m×（2v0）2 -
1
2
×3m×（
 1/2    1 2 下一页 尾页
金属 中点 平板车 知识点 可知
  • 最新内容
  • 相关内容
  • 网友推荐
  • 图文推荐
  • 有一恒力F施与质量为m1的物体上，产(2022-10-29)
  • 如图所示，一油罐车在车的尾部有一(2022-10-29)
  • 如图所示，有两条质量相等的有蓬小(2022-10-29)
  • 一个物体受到一个与它速度方向相同(2022-10-29)
  • 对于质量一定的物体，下列说法正确(2022-10-29)
  • 关于速度、加速度、合力间的关系，(2022-10-29)
  • 如图（a）所示，某人正通过定滑轮将(2022-10-29)
  • 一间新房即将建成时要封顶，考虑到(2022-10-29)
  • 汽车拉着拖车在水平道路上沿直线加(2022-10-29)
  • （附加题）如图甲所示，一边长L=2.5m、质量m=0.5kg的正
  • 如图所示，MN、PQ是平行金属板，板长为L，两板间距离为
  • [选做题]]如图所示，两根正对的平行金属直轨道MN、M′
  • 如图甲所示，A、B两块金属板水平放置，相距为d=0.6cm，
  • 如图所示，质量为m，带电量为-q的小球悬于O点，O点处于
  • 如图（a）所示，电子从加速电场的O点发出（初速不计）
  • 长为1m的轻绳，当受到大小为50N的拉力时会被拉断，现在
  • 如图所示，将一根光滑的细金属棒折成V形，顶角为2θ，
  • 如图所示，两光滑平行导轨MN、PQ水平放置在匀强磁场中
  • 如图是放置在竖直平面内游戏滑轨的模拟装置，滑轨由四
  • 有两支最小分度相同的刻度尺A和B，(2022-10-29)
  • 雨滴从高空由静止下落，若空气对它(2022-10-29)
  • 如图所示，一质量为m、带电量为q的(2022-10-29)
  • 一个物体受到一个与它速度方向相同(2022-10-29)
  • 关于力、加速度、质量之间的关系，(2022-10-29)
  • 关于运动和力的关系，下列说法中正(2022-10-29)
  • 两个完全相同的物块a、b，在水平面(2022-10-29)
  • 滑沙运动起源于非洲，是一种独特的(2022-10-29)
  • 如图在xoy坐标系第Ⅰ象限，磁场方向(2022-10-29)
  • A、B两列火车，在同一轨道上同向行(2022-10-29)
    • 如图所示，一质量为m、带电量为q的物体处于场强按E=E0-kt（E0、k均为大于零的常数，取水平向左为正方向）变化的电场中，物体与竖直墙壁间动摩擦因数为μ，当t=0时刻物体处于静止
    如图所示，一质量为m、带电量    		一个物体受到一个与它速度方向相同、随时间变化如图所示的力的作用，物体的速度、加速度的变化情况是[]A．加速度逐渐增大，速度逐渐增大B．加速度逐渐增大，速度逐渐减小C．加速
    一个物体受到一个与它速度方    		两个完全相同的物块a、b，在水平面上以相同的初速度从同一位置开始运动，图中a直线表示a物体不受拉力作用、b直线表示b物体受到水平拉力F=1.8N作用的υ-t图象，求：（1）a、b运动
    两个完全相同的物块a、b，在    		滑沙运动起源于非洲，是一种独特的体育游乐项目，现在我国许多地方相继建立了滑沙场，滑沙已成为我国很受欢迎的旅游项目．如图所示，运动员从A点沿斜坡由静止开始下滑，经过B
    滑沙运动起源于非洲，是一种    		如图在xoy坐标系第Ⅰ象限，磁场方向垂直xoy平面向里，磁感应强度大小均为B=1.0T；电场方向水平向右，电场强度大小均为E=3N/C．一个质量m=2.0×10-7kg，电荷量q=2.0×10-6C的带
    如图在xoy坐标系第Ⅰ象限，磁
    上一篇：如图是放置在竖直平面内游戏滑轨的模拟装置，滑轨由四部分粗细均匀的金属杆组成：水平直轨AB，半径分别为R1=1.0m和R2=3.0m的弧形轨道APC和BQD，倾斜直轨CD长为L=6m，AB、CD     下一篇：如图所示，在水平面直线MN的上方有一方向与MN成30°角的斜向右下方的匀强电场，电场区域足够宽，场强大小为E．在MN下方有一半径为R的圆形区域，圆心为O，圆O与MN相切于D点，圆
    零零教育社区：论坛热帖子
    栏目导航
    Copyright 2021 零零教育信息网 @ Powered By 零零教育信息网 ，这是一个公共的免费分享平台
    网站导航联系我们广告合作豫ICP备09039788号
    个人中心
    服务邮箱

    服务邮箱

    7720015@qq.com

    微信咨询
    我的网站名称
    返回顶部
    X我的网站名称

    截屏，微信识别二维码

    微信号：ten00_cn

    （点击微信号复制，添加好友）

      打开微信

    微信号已复制，请打开微信添加咨询详情！