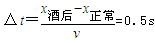如图所示为一传送带的模型,传送带水平部分AB长度L在0.5m<L<2.0m的范围内取值,AB距水平地面的高度h=0.45m,皮带轮顺时针匀速转动使传送带总保持v=2.0m/s的速度匀速运动
◎ 题目
| 如图所示为一传送带的模型,传送带水平部分AB长度L在0.5m<L<2.0m的范围内取值,AB距水平地面的高度h=0.45m,皮带轮顺时针匀速转动使传送带总保持v=2.0m/s的速度匀速运动.现将一工件(可视为质点)从静止轻放在A端,一段时间后工件运动到B端并从B端水平抛出,已知工件与皮带之间的动摩擦因数μ=0.20,g取10m/s2. (1)求工件做加速运动过程的加速度大小; (2)工件从B端水平抛出,B端所在的主动轮半径r应满足什么条件? (3)试讨论工件的落地点与B点的水平距离x与AB长度L的关系.  |
◎ 答案
| (1)根据牛顿第二定律得,f=μmg=ma 解得a=μg=2.0m/s2 (2)由题意得,L=0.5m时,工件仍能水平抛出 工件一直加速,v′2=2aL得v′=
工件恰好水平抛出,有:mg=m
所以r≤0.2m. (3)工件一直匀加速且抛出时的速度等于v,AB的长度为L1 此时v2=2aL1,得L1=1m. 落地点与B点的水平距离x=vt=v
当L≥1.0m时,工件的落地点与B点的水平距离x=0.6m. 当AB的长度为L2=0.5m时,由v′=
知落地点与B点的水平距离x′=v′t=0.3
0.5m<L<1.0m时,水平距离0.3
且由v2=2aL知,v=2
综上所述,0.5m<L<1.0m时,x=vt=0.6
|