如图所示,一质量为M=5.0kg的平板车静止在光滑水平地面上,平板车的上表面距离地面高为h,其右侧足够远处有一障碍物A,另一质量为m=2.0kg可视为质点的滑块,以v0=8m/s的初
◎ 题目
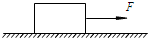
如图所示,一质量为M=5.0kg的平板车静止在光滑水平地面上,平板车的上表面距离地面高为h,其右侧足够远处有一障碍物A,另一质量为m=2.0kg可视为质点的滑块,以v0=8m/s的初速度从左端滑上平板车,同时对平板车施加一水平向右、大小为5N的恒力F,当滑块运动到平板车的最右端时,二者恰好相对静止,此时撤去恒力F,当平板车碰到障碍物A时立即停止运动,滑块水平飞离平板车后,恰能无碰撞地沿圆弧切线从B点切入光滑竖直圆弧轨道,并沿轨道下滑,已知滑块与平板车间的动摩擦因数μ=0.5,圆弧半径为R=2m,圆弧所对的圆心角∠BOD=θ=106°,取g=10m/s2,sin53°=0.8,cos53°=0.6,求:(1)平板车的长度;(2)障碍物A与圆弧左端B的水平距离.(3)滑块在C点处对轨道的压力大小是多少? |
◎ 答案
(1)对滑块,由牛顿第二定律得a1=
对平板车,由牛顿第二定律得 a2=
设经过时间t1,滑块与平板车相对静止,共同速度为υ, 则υ=υ0-a1t1=a2t1 解得 t1=1s υ=3m/s 滑块与平板车在时间t1内通过的位移分别为 x1=
x2=
则平板车的长度为 L=x1-x2=
(2)设滑块从平板车上滑出后做平抛运动的时间为t2,因滑块恰能无碰撞地沿圆弧切线从B点切入光滑竖直圆弧轨道, 对B处速度进行分解可知: tan53°=
又υx=υ=3m/s 得υy=4m/s 由公式υy=gt2xAB=υxt2 解得xAB=1.2m (3)在B点的速度的大小为 υB=
由B到C过程中由机械能守恒定律得:
在C点处,由牛顿第二定律得:N-mg= |