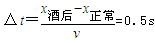如图所示,O为竖直平面内14圆弧轨道的圆心,B点的切线刚好沿水平方向.一个质量为m的滑块(可视为质点)从A点由静止开始滑下,最终落到地面上的C点.已知A点离地面的高度为h,圆
◎ 题目
如图所示,O为竖直平面内
(1)滑块经B点时的速度大小; (2)滑块经B点时对轨道的压力; (3)在保证A点位置不变的情况下,改变圆弧轨道 的半径(总小于h),再让滑块从A点由静止滑下,A点到滑块落地点的水平距离最大是多少?此时圆弧轨道的半径是多大?  |
◎ 答案
(1)滑块从A到B的过程中,由机械能守恒得mgR=
解得 vB=
(2)滑块经B点时,由向心力公式有N-mg=m
解得 N=3mg 由牛顿第三定律知,滑块经B点时对轨道的压力大小为3mg,方向竖直向下. (3)设轨道半径为r,滑块从B点开始做平抛运动,需时间t落地,则h-r=
平抛的水平距离 xBC=vBt 联立解得A、C两点的水平距离为 xAC=r+xBC=r+2
令r=hsin2θ,则AC两点的水平距离为xAC=h(sin2θ+2sinθcosθ)=h(
令tanφ=
显然当θ=
上一篇:美国通用汽车公司推出的“氢气Ⅰ型”汽车是一种使用燃料电池驱动的电动汽车,它用氢气和氧气直接反应,其生成物只有水,因此对环境没有污染.若该车质量为1.5×103kg,额定功率为
下一篇:如图所示,悬挂在竖直平面内O点的一个木质小球(可以看成质点),悬线长为L,小球的质量为M.一颗质量为m的子弹,以水平速度v0射入木球且留在其中,随即木球就在竖直平面内运动
零零教育社区:论坛热帖子
|