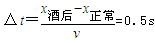v B和

v

C

，则有

v

A

＞

v

B

    

v

B

=

v

C

      （8）
在物块A、B发生碰撞的极短时间内，木板C对它们的摩擦力的冲量非常小，可忽略不计．故在碰撞过程中，A与B构成的系统动量守恒，而木板C的速度保持不变，因为物块A、B间的碰撞是弹性的，系统的机械能守恒，又因为质量相等，由动量守恒和机械能守恒可以证明（证明从略），碰撞前后A、B交换速度，若碰撞刚结束时，A、B、C三者速度分别为

v

′A

、

v

′B

和

v

′C

，则有

v

′A

=

v

B

   

v

′B

=

v

A

   

v

′C

=

v

C

    （9）
由（8）、（9）式可知，物块A与木板C速度相等，保持相对静止，B相对AC向右运动，以后发生的过程相当于第1问中所进行的延续，由物块B代替A继续向右运动．
若物块B刚好与挡板P不发生碰撞，则物块B以速

v

′B

从C板的中点运动到挡板P所在处时与C的速度相等．A与C的速度大小是相等的，A、B、C三者的速度相等，设此时三者的速度

v

2

，根据动量守恒定律有m

v

0

=3m

v

2

    （10）
A以初速度

v

0

开始运动，接着与B发生完全弹性碰撞，碰撞后物块A相对木板C静止，B到达P所在处这一整个过程中，先是A相对C运动的路程为L，接着是B相对C运动的路程为L，整个系统动能的改变，等于系统内部相互间的滑动摩擦力做功的代数和，即

1

2

（3m）

v

22

-

1

2

m

v

20

=-μmg.2L        （11）
解（10）、（11）两式得  

v

0

=

3/8   首页 上一页 1 2 3 4 5 6 下一页 尾页 木板 之间 中点 代数和 施加 最新内容 相关内容 网友推荐 图文推荐 如图所示，光滑的平行导轨倾角为θ(2022-10-29) 如图所示，在水平桌面上放有长木板(2022-10-29) 一单摆做小角度摆动，其振动图象如(2022-10-29) 如图所示，电源电动势E=60V，内阻r(2022-10-29) 如图所示为一圆拱桥，最高点的半径(2022-10-29) 一根长为L的轻杆下端固定一个质量为(2022-10-29) 如图所示，圆形区域的匀强磁场，磁(2022-10-29) 如图所示，两足够长平行光滑的金属(2022-10-29) 平板小车静止在光滑的水平面上，其(2022-10-29) 某同学在探究木箱与水平地面之间的摩擦情况时，做了如 如图所示，传送带与水平面之间的夹角为θ=30°，其上A 如图甲所示，在两极板a、b之间有一静止的电子，当在a、 如图所示，质量为m、电量为q的带正电小球，可在半径为 如图所示的坐标系，在y轴左侧有垂直纸面、磁感应强度为 如图所示，能发射电子的阴极k和金属板P之间所加电压为 两木块的质量之比为3：2，初速度之比为2：3，它们在同 如图所示，相距为d的平行金属板A、B竖直放置，在两板之 水平地面上放置一个质量为M的木箱，箱中的顶端用一长为 如图所示，电源电动势E=60V，内阻r=1Ω，R1=3Ω，R2=6 有两支最小分度相同的刻度尺A和B，(2022-10-29) 雨滴从高空由静止下落，若空气对它(2022-10-29) 如图所示，一质量为m、带电量为q的(2022-10-29) 酒后驾驶会导致许多安全隐患，是因(2022-10-29) 如图所示，小球从高处下落到竖直放(2022-10-29) 如图所示，一个质量m=20kg的物体放(2022-10-29) 如图，纸面内有E、F、G三点，∠GEF(2022-10-29) 如图所示，A、B（可视为质点）质量(2022-10-29) 如图所示，弹簧左端固定，右端自由(2022-10-29) 在游乐场中有一种旋转飞椅，如图所(2022-10-29) 如图所示，一质量为m、带电量 酒后驾驶会导致许多安全隐患 如图所示，小球从高处下落到 如图所示，一个质量m=20kg的 如图，纸面内有E、F、G三点， 上一篇：一单摆做小角度摆动，其振动图象如图，以下说法正确的是（）A．t1时刻摆球速度最大，悬线对它的拉力最小B．t2时刻摆球速度为零，悬线对它的拉力最小C．t3时刻摆球速度为零，悬线对     下一篇：如图所示，光滑的平行导轨倾角为θ，处在磁感应强度为B的匀强磁场中，导轨中接入电动势为E、内阻为r的直流电源．电路中有一阻值为R的电阻，其余电阻不计，将质量为m、长为L的导 零零教育社区：论坛热帖子 [高考] 2022 西安电子科技大学《软件工程》大作业答案 (2022-04-25) [家长教育] 孩子为什么会和父母感情疏离？ (2019-07-14) [教师分享] 给远方姐姐的一封信 (2018-11-07) [教师分享] 伸缩门 (2018-11-07) [教师分享] 回家乡 (2018-11-07) [教师分享] 是风味也是人间 (2018-11-07) [教师分享] 一句格言的启示 (2018-11-07) [教师分享] 无规矩不成方圆 (2018-11-07) [教师分享] 第十届全国教育名家论坛有感（二） (2018-11-07) [教师分享] 贪玩的小狗 (2018-11-07) 栏目导航 质点 参考系 坐标系 时刻和时间 路程和位移 速度和速率的区别 平均速度和瞬时速度的区别 速度的定义式 加速度 加速度和速度的关系 矢量和标量 机械运动 匀速直线运动 打点计时器 实验：探究小车速度随时间变化的规律 匀变速直线运动的速度与时间的关系 匀变速直线运动的位移与时间的关系 匀变速直线运动的位移与速度的关系 匀变速直线运动规律的应用 匀变速直线运动的导出公式 匀变速直线运动 自由落体运动 伽利略对自由落体运动的研究 竖直上抛运动 v-t图像 s-t图像 其他运动图像 游标卡尺 螺旋测微器 运动的合成与分解 平抛运动 斜抛运动 实验：研究平抛运动 线速度 角速度 周期、频率、转速 向心加速度 向心力 匀速圆周运动 弯道 拱桥 航天器中的失重 离心运动 圆锥摆 生活中的其他圆周运动 认识曲线运动 开普勒行星运动定律 万有引力定律的推导 计算天体质量与密度 发现未知天体 人造地球卫星 地球同步卫星 万有引力定律的其他应用 宇宙速度 经典力学的局限性 万有引力定律 万有引力常量 力的概念 受力分析 力的图示和力的示意图 重力的产生、方向和大小 重心 形变和弹性形变 弹力的产生、方向和种类 弹力的大小、胡克定律 实验：探究弹力与弹簧伸长的关系 静摩擦力 滑动摩擦力、动摩擦因数 力的合成 力的分解 共点力的平衡 实验：验证力的平行四边形定则 四种基本相互作用 力矩的平衡 对力和运动关系的探究 牛顿第一定律 惯性 实验：探究加速度与力、质量的关系 从受力确定运动情况 从运动情况确定受力 超重 失重 牛顿第二定律 牛顿运动定律的应用 力学单位制 平衡力 作用力和反作用力 牛顿第三定律 功 正功和负功的区别 功率 额定功率和实际功率的区别 平均功率和瞬时功率的区别 重力势能 弹性势能 实验：探究功与速度变化的关系 动能 动能定理 机械能 机械能守恒定律 实验：验证机械能守恒定律 功能关系 能量转化与守恒定律 能量守恒的探究 动量 冲量 动量定理 碰撞 反冲运动 爆炸 动量守恒定律 动量守恒定律的应用 实验：验证动量守恒定律 简谐运动的概念 简谐运动的图像 简谐运动的表达式 简谐运动的位移和路程 简谐运动的振幅 简谐运动的周期、频率和角频率 简谐运动的初相、相位和相位差 简谐运动的回复力和能量 弹簧振子 单摆的回复力 单摆的周期 实验：用单摆测定重力加速度 实验：探究单摆周期与摆长的关系 阻尼振动 受迫振动 共振 机械波的形成和传播 横波与纵波 波的图像 波长、频率和波速 惠更斯原理 波的反射 波的折射 波的衍射 波的叠加 波的干涉 多普勒效应 超声波和次声波 电荷、元电荷 摩擦起电、接触起电、感应起电 电荷守恒定律 库仑定律 电场线 匀强电场 电场强度的定义式 点电荷的电场强度 电场强度的叠加 电场、电场力 电势能 电势 等势面 实验：用描迹法画出电场中平面上的等势线 电势差 电势差与电场强度的关系 电场力的功 生活中的静电现象 静电平衡状态、等势体 静电屏蔽 电容的定义式 平行板电容器 常用电容器 电容器的概念和原理 带电粒子在电场中的加速 带电粒子在电场中的偏转 示波管 带电粒子在电场中运动的综合应用 实验：练习使用示波器 电源 电流 电动势、内阻 欧姆定律 实验：测绘小灯泡的伏安特性曲线 实验：伏安法测电阻 串联电路的电流、电压和电阻 并联电路的电流、电压和电阻 半偏法测电表的内阻 表头的改装 电路问题分析 电功 电功率 焦耳定律，电热 热功率 电流的热效应 电阻定律、电阻率 实验：探究影响导体电阻的因素 实验：测定金属的电阻率 路端电压 闭合电路的功率 闭合电路欧姆定律 实验：练习使用多用电表 实验：用多用电表探测黑箱内的电学元件 实验：测定电池的电动势和内阻 逻辑电路 半导体和超导体 集成电路 光敏电阻 热敏电阻和金属热电阻 霍尔元件 传感器及其工作原理 传感器的应用 实验：传感器的应用 磁现象 磁性材料 电流的磁效应 电流的磁场，安培定则 匀强磁场 安培分子电流假说 磁感应强度 磁场对通电导线的作用：安培力、左手定则 磁电式仪表 电动机 磁场对运动电荷的作用：洛伦兹力、左手定则 显像管 带电粒子在匀强磁场中的运动 质谱仪 回旋加速器 带电粒子在复合场中的运动 磁场，地磁场 磁感线 磁通量 探究产生感应电流的条件 楞次定律 右手定则 感应电流 法拉第电磁感应定律 导体切割磁感线时的感应电动势 感应电动势 电磁感应现象中的磁变类问题 电磁感应现象中的切割类问题 电磁感应现象的综合应用 互感现象 自感现象 生活中的电磁感应现象 对电和磁联系的探究 交变电流的产生 正弦式交变电流 交变电流的周期和频率 交变电流的最大值、有效值、瞬时值和平均值 交变电流的相位和相位差 交变电流的图像 电感器对交变电流的作用 电容器对交变电流的作用 变压器的结构和原理 变压器电压、电流、电功率与匝数的关系 高压输电、电网供电 远距离输电的相关计算 三相交变电流 交流发电机 麦克斯韦的电磁场理论 电磁波 电磁振荡的产生 电磁振荡的周期和频率 无线电波的发射、接收和传播 电磁波与信息化社会 电磁波谱 分子的大小 实验：用油膜法估测分子的大小 阿伏伽德罗常数 扩散现象 布朗运动 分子热运动 分子间的相互作用力 温度和温标 分子动能 分子势能 物体的内能 分子动理论 分子热运动的统计规律 做功和内能 热传递和内能 能量守恒定律、第一类永动机 热力学第一定律 第二类永动机 热力学第二定律 热力学第三定律，绝对零度 有序和无序 熵增加原理 热机 能源与可持续发展 气体的压强 玻意耳定律（等温定律） 查理定律（等容定律） 盖—吕萨克定律（等压定律） 理想气体 理想气体状态方程 气体温度的微观意义 气体压强的微观意义 气体实验定律的微观解释 气体分子运动特点 晶体和非晶体 晶体的微观结构 液体的微观结构 液体的表面张力 浸润和不浸润 毛细现象 液晶 饱和汽与饱和汽压 空气的湿度 物态变化中的能量交换 光的直线传播 光的反射定律 光的折射定律 折射率 实验：测定玻璃的折射率 全反射，临界角 全反射棱镜 光导纤维 光的色散 光谱 透镜 光源 双缝干涉 双缝干涉中决定明暗条纹的条件 薄膜干涉 光的干涉在技术中的应用 双缝干涉中计算波长的公式 实验：用双缝干涉测量光的波长 光的衍射 光的偏振 激光 能量量子化 光电效应实验规律 爱因斯坦的光子说 光电效应方程 康普顿效应 光子的动量 粒子的波动性，德布罗意波 概率波 不确定性关系 光的波粒二象性 电子的发现 X射线 α、β、γ射线 天然放射现象 原子的核式结构模型：α粒子散射实验 原子核的组成 同位素 氢原子光谱 玻尔的原子理论 氢原子的能级 α衰变 β衰变 半衰期 碳14鉴年技术 探测射线的方法 放射性的应用与防护 核反应 核能，爱因斯坦质能方程 核能的利用：核电站、核武器 重核裂变 轻核聚变 粒子和宇宙 经典相对性原理 时间和空间的相对性 狭义相对论的其他结论 广义相对论 狭义相对论的两个基本假设 最新信息 如图所示，光滑的平行导轨倾角为θ 如图所示，在水平桌面上放有长木板 一单摆做小角度摆动，其振动图象如 如图所示，电源电动势E=60V，内阻r 如图所示为一圆拱桥，最高点的半径 一根长为L的轻杆下端固定一个质量为 如图所示，圆形区域的匀强磁场，磁 如图所示，两足够长平行光滑的金属 平板小车静止在光滑的水平面上，其 如图所示，质量为m=lkg的小球穿在斜 热门信息 有两支最小分度相同的刻度尺A和B， 雨滴从高空由静止下落，若空气对它 如图所示，一质量为m、带电量为q的 酒后驾驶会导致许多安全隐患，是因 如图所示，小球从高处下落到竖直放 如图所示，一个质量m=20kg的物体放 如图，纸面内有E、F、G三点，∠GEF 如图所示，A、B（可视为质点）质量 如图所示，弹簧左端固定，右端自由 在游乐场中有一种旋转飞椅，如图所 Copyright 2021 零零教育信息网 @ Powered By 零零教育信息网 ，这是一个公共的免费分享平台 网站导航联系我们广告合作豫ICP备09039788号 个人中心 服务邮箱 服务邮箱 7720015@qq.com 微信咨询 返回顶部 网站首页 联系我 微信咨询 个人中心 X 截屏，微信识别二维码 微信号：ten00_cn （点击微信号复制，添加好友）   打开微信 微信号已复制，请打开微信添加咨询详情！ 新闻 图书