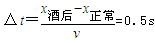沿水平方向的场强为E=8.66×103v/m的足够大的匀强电场中，用绝缘细线系一个质量m=6.0g的带电小球，线的另一端固定于O点，平衡时悬线与竖直方向成30°角，如图所示，求：（1）小

首页 > 考试 > 物理 > 高中物理 > 牛顿第二定律/2022-10-29 / 加入收藏 / 阅读 [打印]

◎ 题目

沿水平方向的场强为E=8.66×103v/m的足够大的匀强电场中，用绝缘细线系一个质量m=6.0g的带电小球，线的另一端固定于O点，平衡时悬线与竖直方向成30°角，如图所示，求：
（1）小球所带的电量
（2）剪断细线小球怎样运动，加速度多大？（g取10m/s2）
魔方格

◎ 答案

（1）对小球受力分析，受到重力、电场力和细线的拉力，如图

魔方格

根据共点力平衡条件，有
T=
mg
cos30°
=
2

3
3
mg
qE=mgtan30°
解得
q=
mgtan30°
E
=
6×10-2×

3
3
8.66×103
=4×10-6C
即小球所带的电量为4×10-6C．
（2）剪断细线后，重力和电场力不变，故合力沿着之前细线的反方向，大小为
2

3
3
mg
根据牛顿第二定律，有
2

3
3
mg=ma
解得
a=
2

3
3
g
即剪断细线小球将沿着细线反方向做匀加速直线运动，加速度为
2

 1/2    1 2 下一页 尾页
竖直 知识点 绝缘 足够 固定
  • 最新内容
  • 相关内容
  • 网友推荐
  • 图文推荐
  • 将质量为16kg的木箱放在水平地面上(2022-10-29)
  • 沿水平方向的场强为E=8.66×103v/m(2022-10-29)
  • 加速上升的电梯顶部悬有一轻质弹簧(2022-10-29)
  • 一种氢气燃料的汽车，质量为m=2.01(2022-10-29)
  • 如图所示，半径分别为R和r的甲、乙(2022-10-29)
  • 如图所示，将完全相同的两小球A、B(2022-10-29)
  • 一个质量为50kg的人乘电梯竖直向上(2022-10-29)
  • 一物体以初速度v1从地面竖直上抛，(2022-10-29)
  • 如图所示，水平地面上的平板车在外(2022-10-29)
  • 如右图所示的箱子中，用OA、OB两根绳子吊着一个质量为
  • 如图所示的“S”形玩具轨道，该轨道是用内壁光滑的薄壁
  • 如图所示，倾角为37°、足够长的斜面体固定在水平地面
  • 如图所示，长0.5m的轻质细杆，一端固定有一个质量为3k
  • 如图所示，在一根长1.5L的不能伸长的轻绳上，穿一个质
  • 如图所示，轻绳长为L一端系一小球，另一端固定于O点，
  • 质量为m的物块，沿着半径为R的半球形金属壳内壁滑下，
  • 一物体以初速度v1从地面竖直上抛，由于空气阻力作用，
  • 一个质量为50kg的人乘电梯竖直向上运行，如图为电梯的
  • 如图所示，半径分别为R和r的甲、乙两个光滑的圆形轨道
  • 有两支最小分度相同的刻度尺A和B，(2022-10-29)
  • 雨滴从高空由静止下落，若空气对它(2022-10-29)
  • 如图所示，一质量为m、带电量为q的(2022-10-29)
  • 酒后驾驶会导致许多安全隐患，是因(2022-10-29)
  • 如图所示，小球从高处下落到竖直放(2022-10-29)
  • 如图所示，一个质量m=20kg的物体放(2022-10-29)
  • 如图，纸面内有E、F、G三点，∠GEF(2022-10-29)
  • 如图所示，A、B（可视为质点）质量(2022-10-29)
  • 如图所示，弹簧左端固定，右端自由(2022-10-29)
  • 在游乐场中有一种旋转飞椅，如图所(2022-10-29)
    • 如图所示，一质量为m、带电量为q的物体处于场强按E=E0-kt（E0、k均为大于零的常数，取水平向左为正方向）变化的电场中，物体与竖直墙壁间动摩擦因数为μ，当t=0时刻物体处于静止
    如图所示，一质量为m、带电量    		酒后驾驶会导致许多安全隐患，是因为驾驶员的反应时间变长，反应时间是指驾驶员从发现情况到采取制动的时间．下表中“思考距离”是指驾驶员从发现情况到采取制动的时间内汽车行
    酒后驾驶会导致许多安全隐患    		如图所示，小球从高处下落到竖直放置的轻弹簧上，从接触弹簧开始到将弹簧压缩到最短的过程中，下列传述正确的是（）A．小球的速度一直减小B．小球的加速度先减小后增大C．小球的加
    如图所示，小球从高处下落到    		如图所示，一个质量m=20kg的物体放在光滑水平地面上．对物体施加一个F=10N的水平拉力，使物体由静止开始做匀加速直线运动．求：（1）物体在4.0s时间内的位移大小；（2）拉力F在4.
    如图所示，一个质量m=20kg的    		如图，纸面内有E、F、G三点，∠GEF=30°，∠EFG=135°．空间有一匀强磁场，磁感应强度大小为B，方向垂直于纸面向外．先使带有电荷量为q（q＞0）的点电荷a在纸面内垂直于EF从F点射出，
    如图，纸面内有E、F、G三点，
    上一篇：加速上升的电梯顶部悬有一轻质弹簧，弹簧下端挂有一铁块，若电梯突然停止，以电梯底板为参照物，铁块在继续上升的过程中（）A．动能先增大后减小B．动能逐渐减小C．加速度逐渐增大     下一篇：将质量为16kg的木箱放在水平地面上，木箱和地面间的动摩擦因数μ=0.2，用一个与水平面成37°角斜向右上方的力F拉这个木箱，使木箱从静止开始做匀加速直线运动．经过10s，速度变
    零零教育社区：论坛热帖子
    栏目导航
    Copyright 2021 零零教育信息网 @ Powered By 零零教育信息网 ，这是一个公共的免费分享平台
    网站导航联系我们广告合作豫ICP备09039788号
    个人中心
    服务邮箱

    服务邮箱

    7720015@qq.com

    微信咨询
    我的网站名称
    返回顶部
    X我的网站名称

    截屏，微信识别二维码

    微信号：ten00_cn

    （点击微信号复制，添加好友）

      打开微信

    微信号已复制，请打开微信添加咨询详情！