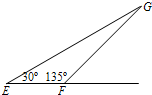
如图所示,光滑的平行金属导轨CD与EF间距为L=lm,与水平夹角为θ=30°,导轨上端用导线CE连接(导轨和连接线电阻不计),导轨处在磁感应强度为B=0.1T、方向垂直于导轨平面向上的
axxR
ax,
则得kgsinθ-
=kax,①
从上述方程可以看出的解ax是一个定值,与位移x无关,这表明前面的假设成立,棒的运动确实是匀加速直线运动.若ax与位移x有关,则说明ax是一个变量,即前面的假设不成立.
(3)为了求棒下滑2m时的速度,应先求出棒的加速度.将题目给出的数据代①式得到
0.1×10×
-
=0.1a
化简得 10a+
?
-50=0
令y=
,则得 y2+
y-50=0
解得,a=4.69m/s2
根据匀变速运动规律,v=
=
| x |
则得kgsinθ-
B2L2
| ||
| R |
从上述方程可以看出的解ax是一个定值,与位移x无关,这表明前面的假设成立,棒的运动确实是匀加速直线运动.若ax与位移x有关,则说明ax是一个变量,即前面的假设不成立.
(3)为了求棒下滑2m时的速度,应先求出棒的加速度.将题目给出的数据代①式得到
0.1×10×
| 1 |
| 2 |
| ||
| 1 |
| a |
化简得 10a+
| 2 |
| a |
令y=
| a |
| 2 |
解得,a=4.69m/s2
根据匀变速运动规律,v=
| 2axx |