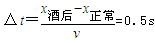如图所示,水平x轴是匀强电场的上边界线,xoy平面内的竖直线PQ是匀强电场、匀强磁场的分界线,匀强电场的方向竖直向上,匀强磁场的方向垂直于xoy平面向里(磁感应强度大小B未
◎ 题目
如图所示,水平x轴是匀强电场的上边界线,xoy平面内的竖直线PQ是匀强电场、匀强磁场的分界线,匀强电场的方向竖直向上,匀强磁场的方向垂直于xoy平面向里(磁感应强度大小B未知).质量为m、电荷量为q的带正电质点自y轴上的A(0,L)点以初速度v0水平向右抛出,经过一段时间后垂直于竖直线PQ射入匀强磁场.已知重力加速度为g,匀强电场的电场强度大小E=
(1)求竖直线PQ与y轴之间可能的距离; (2)若使带电质点在竖直线PQ右侧区域作半径为L的匀速圆周运动,试指出在该区域应添加匀强电场E1的方向,并分别求出电场强度E1、磁感应强度B的大小; (3)在(2)问情形下,质点自A点抛出后经多长时间回到y轴?  |
◎ 答案
 (1)质点自A点抛出后先作平抛运动 x0=v0t L=
∴水平位移x0=v0
接着在重力、电场力作用下作匀变速曲线运动, 设加速度为a,根据牛顿第二定律qE-mg=ma得 a=g 根据对称性可知,运动轨迹与上一过程的运动轨迹为中心对称图形,如上图所示. 所以,竖直线PQ与y轴之间可能的距离x=n×2x0=2nv0
(2)若使带电质点在竖直线PQ右侧区域作半径为L的匀速圆周运动,应满足:qE1=mg,qv0B=
所以,电场强度的大小:E1=
磁感应强度的大小:B=
(3)时间:t=tE+tB+tE=
|