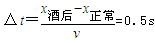如图所示,质量为m、边长为L的正方形金属线框,放在倾角为θ的光滑足够长的斜面的底端,整个装置处在与斜面垂直的磁场中,在斜面内建立图示直角坐标系,磁感应强度在x轴方向分
◎ 题目
| 如图所示,质量为m、边长为L的正方形金属线框,放在倾角为θ的光滑足够长的斜面的底端,整个装置处在与斜面垂直的磁场中,在斜面内建立图示直角坐标系,磁感应强度在x轴方向分布均匀,在y轴方向分布为B=B0+ky(k为大于零的常数).现给线框沿斜面向上的初速度v0,经时间t0线框到达最高点,然后开始返回,到达底端前已经做匀速运动,速度大小为v0/4.已知线框的电阻为R,重力加速度为g.求: (1)线框从开始运动到返回底端的过程中,线框中产生的热量; (2)线框在底端开始运动时的加速度大小; (3)线框上升的最大高度.  |
◎ 答案
| (1)线框从开始运动到返回底端的过程中,线框的动能减小转化为内能,根据能量守恒得: Q=
(2)感应电动势:E=△BLv0=k△yLv0=kL2v0 感应电流:I=
合安培力:F=△BIL=k△yIL=kIL2=
根据牛顿第二定律:mgsinθ+F=ma 得:a=gsinθ+
(3)在上升过程中,由牛顿第二定律,得:mgsinθ+
又a=
mgsinθ+
mgsinθ?△t+
两边求和得: |