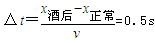如图所示，斜面与水平面在B点衔接，水平面与竖直面内的半圆形导轨在C点衔接，半圆形导轨的半径为r=0.4m．质量m=0.50kg的小物块，从A点沿斜面由静止开始下滑，测得它经过C点-00教育-零零教育信息网

濠殿喗锚閻°劌危閹间焦鍎戦柛蹇曞帶閻ㄧ偓淇婇锝勬倣缂佽鲸绻勬禒锔芥綇閵娤€锕傛煟椤忓嫷妲搁柛銏＄叀閹虫洖顫濋妷銏犱壕闁稿本渚楅崕姗€姊婚崒銈呮灕妞ゃ垺鍨剁粋宥夊传閸曨偆顔岄梻渚囧弿缂嶁偓缂佹梻鍠栭弫宥夋偄閻戞ḿ鐣抽梺娲讳海閸嬫劕鈻旈埡鍛剮闁割偅绻嶅Σ閬嶆煏閸℃鈧鏅堕悩铏弿閻庯綆鍠掗崑鎾存媴鐟欏嫅姘辨喐閻楀牆閲滅紒杈ㄧ箞瀹曪綁宕奸妷銏犱壕濞达絽鎲￠崑妯兼喐閻楀牆绗掓鐐存崌婵℃挳宕掑┑鍡╀户闂佸憡甯炴晶妤呮儓濞嗘挸纭€婵°倕瀚崹浣糕槈閹剧鏀绘俊宸墴閺佸秶浠﹂挊澶岋紟婵炴垶鎸稿ú銈夊箯娴兼潙鍙婇柕澶堝€楃粔鍫曟煏閸☆厽瀚�

如图所示，斜面与水平面在B点衔接，水平面与竖直面内的半圆形导轨在C点衔接，半圆形导轨的半径为r=0.4m．质量m=0.50kg的小物块，从A点沿斜面由静止开始下滑，测得它经过C点

首页 > 考试 > 物理 > 高中物理 > 牛顿第二定律/2022-10-29 / 加入收藏 / 63 阅读 [打印]

◎ 题目

如图所示，斜面与水平面在B点衔接，水平面与竖直面内的半圆形导轨在C点衔接，半圆形导轨的半径为r=0.4m．质量m=0.50kg的小物块，从A点沿斜面由静止开始下滑，测得它经过C点进入半圆形导轨瞬间对导轨的压力为35N，之后向上运动恰能完成半圆周运动到达D点．已知A到B的水平距离为l₁=3.2m，B到C的水平距离为l₂=1.6m，物块与斜面及水平面之间的动摩擦因数均为μ=0.25，不计物块通过衔接点时的能量损失，g取10m/s²．
求：
（1）物块从C至D克服阻力做了多少功？
（2）A点离水平面的高度h为多大？
（3）为使物块恰好不能越过C而进入半圆形导轨内，物块在斜面上下滑的起始高度应调节为多大？

◎ 答案

（1）圆周运动在C点有，N-mg=m

①
圆周运动在D点有，mg=m

②
从C至D由动能定理有，-mg?2r-W_f=

③
联立①②③式并代入数据可解得，从C至D物块克服阻力做的功W_f=1J ④
（2）从A到B过程，物块克服阻力做的功W1=μmgcosθ?

cosθ

=μmgl1 ⑤
从A到C，由动能定理有，mgh-W1-μmgl2=

-0⑥
联立①⑤⑥式并代入数据可解得，h=2.4m⑦
（3）从起始到C点由动能定理有，mgh′-μmgcosθ?

h′

sinθ

-μmgl2=0⑧
又

sinθ

cosθ

h′

⑨
联立⑧⑨式并代入数据可解得，h'=0.6m
答：
（1）物块从C至D克服阻力做了1J功．
（2）A点离水平面的高度h为2.4m．
（3）为使物块恰好不能越过C而进入半圆形导轨内，物块在斜面上下滑的起始高度应调节为0.6m．

◎ 解析

“略”

◎ 知识点

专家分析，试题“如图所示，斜面与水平面在B点衔接，水平面与竖直面内的半圆形导轨在C点衔接，半圆形导轨的半径为r=0.4m．质量m=0.50kg的小物块，从A点沿斜面由静止开始下滑，测得它经过C点…”主要考查了你对【向心力】，【牛顿第二定律】，【动能定理】等知识点的理解和应用能力。关于这些知识点的“档案”，你可以点击相应的链接进行查看和学习。

闁烩剝甯掗幊搴ｇ博閼哥數鐟归柛顭戝枛閻掓椽骞栫€涙ǜ浠︾紒妤€鎳樺畷锟犲即濮樺崬鏋犻梺璇″灲閹凤拷濠殿噯绲界换鎰板Φ婢跺绱ｉ柛鈩冾殔缁插潡鏌涢幒婵嗕喊闁轰礁锕ュḿ濠氬炊妞嬪海顦梺鍛婎殕濞叉牕鐣烽悢绋款嚤婵☆垵顕ч崝鏇灻瑰⿰搴′簵缂佹顦靛畷鎴︽晸閿燂拷