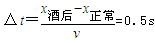飞行时间质谱仪可以对气体分子进行分析.如图所示,在真空状态下,脉冲阀P喷出微量气体,经激光照射产生不同价位的正离子,自a板小孔进入a、b间的加速电场,从b板小孔射出,沿
◎ 题目
| 飞行时间质谱仪可以对气体分子进行分析.如图所示,在真空状态下,脉冲阀P喷出微量气体,经激光照射产生不同价位的正离子,自a板小孔进入a、b间的加速电场,从b板小孔射出,沿中线方向进入M、N板间的偏转控制区,到达荧光屏.已知元电荷电量为e,a、b板间距为d,极板M、N的长度和间距均为L.不计离子重力及进入a板时的初速度. (1)当a、b间的电压为U1时,在M、N间加上的电压为U2,为使离子沿直线到达荧光屏,请导出M、N间所加匀强磁场的磁感应强度B与离子的比荷K(K=
(2)去掉偏转电压U2,在M、N间区域加上垂直于纸面的匀强磁场,磁感应强度为B0.若进入a、b间所有离子质量均为m,要使所有的离子均能通过控制区从右侧飞出打到荧光屏上,a、b间的加速电压U1至少为多少?  |
◎ 答案
(1)n价正离子在a、b加速电场的作用下加速,设进入M、N间的速度为v,由动能定理可得:
进入M、N后没有发生偏转说明电场力与洛沦兹力平衡,故有:
由①②可得:B=
(2)设带电离子在磁场中运动的最小半径为R,由几何关系可得(R-
解得:R=
设离子向心加速度为a,由牛顿第二定律得:nevB0=ma ⑥ 又由于圆周运动得:a=
由⑤⑥⑦解得最小速度为:v=
由①⑧解得加速电压的最小值为: U1=
答:(1)M、N间所加匀强磁场的磁感应强度B与离子的比荷K(K=
|