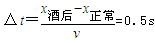在如图所示的竖直平面内,物体A和带正电的物体B用跨过定滑轮的绝缘轻绳连接,分别静止于倾角θ=370的光滑斜面上的M点和粗糙绝缘水平面上,轻绳与对应平面平行.劲度系数K=5N/m
◎ 题目
| 在如图所示的竖直平面内,物体A和带正电的物体B用跨过定滑轮的绝缘轻绳连接,分别静止于倾角θ=370的光滑斜面上的M点和粗糙绝缘水平面上,轻绳与对应平面平行.劲度系数K=5N/m的轻弹簧一端固定在0点,一端用另一轻绳穿过固定的光滑小环D与A相连,弹簧处于原长,轻绳恰好拉直,DM垂直于斜面.水平面处于场强E=5×104N/C、方向水平向右的匀强电场中.已知A、B的质量分别为mA=0.1kg和mB=0.2kg,B所带电荷量q=+4×l0-6C.设两物体均视为质点,不计滑轮质量和摩擦,绳不可伸长,弹簧始终在弹性限度内,B电量不变.取g=lOm/s2,sin37°=0.6,cos37°=0.8. (1)求B所受静摩擦力的大小; (2)现对A施加沿斜面向下的拉力F,使A以加速度a=0.6m/s2开始做匀加速直线运动.A从M到N的过程中,B的电势能增加了△Ep=0.06J.已知DN沿竖直方向,B与水平面间的动摩擦因数μ=0.4.求A到达N点时拉力F的瞬时功率.  |
◎ 答案
| (1)据题意静止时受力分析如图所示 由平衡条件得: 对A有mAgsinθ=FT① 对B有qE+f0=FT② 代入数据得f0=0.4N③ (2)据题意A到N点时受力分析如图所示由牛顿第二定律得: 对A有F+mAgsinθ-FT-FKsinθ=mAa④ 对B有FT-qE-f=mBa⑤ 其中f=μmBg⑥ FK=kx⑦ 由电场力做功与电势能的关系得△EP=qEd⑧ 由几何关系得x=
A由M到N由
拉力F在N点的瞬时功率P=Fv? 由以上各式代入数据P=0.528W? 答:(1)B所受静摩擦力的大小为0.4N. (2)A到达N点时拉力F的瞬时功率为0.528W.  |
◎ 解析
“略”◎ 知识点
专家分析,试题“在如图所示的竖直平面内,物体A和带正电的物体B用跨过定滑轮的绝缘轻绳连接,分别静止于倾角θ=370的光滑斜面上的M点和粗糙绝缘水平面上,轻绳与对应平面平行.劲度系数K=5N/m…”主要考查了你对 【牛顿第二定律】 等知识点的理解和应用能力。关于这些知识点的“档案”,你可以点击相应的链接进行查看和学习。- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
上一篇:一个质量为2kg的物体静止在足够大的水平地面上,物体与地面间的动摩擦因数μ=0.2.从t=0开始,物体受到一个大小和方向呈周期性变化的水平力F的作用,力F随时间的变化规律如图
下一篇:水平桌面上有两个玩具车A和B,两者用一轻质细橡皮筋相连,在橡皮筋上有一红色标记R.在初始时橡皮筋处于拉直状态,A、B和R分别位于直角坐标系中的(0,2l)、(0,-l)和(0,0)点
零零教育社区:论坛热帖子
| [高考] 2022 西安电子科技大学《软件工程》大作业答案 (2022-04-25) |
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |