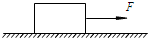
如图所示，倾角θ=37°的斜面足够长，质量m=1kg的滑块静置在斜面的底端A点，滑块与斜面间的动摩擦因素为μ=0.5．现给滑块一个沿斜面向上v°=10m/s的初速度，同时用水平恒力F向右
◎ 题目
| 如图所示，倾角θ=37°的斜面足够长，质量m=1kg的滑块静置在斜面的底端A点，滑块与斜面间的动摩擦因素为μ=0.5．现给滑块一个沿斜面向上v°=10m/s的初速度，同时用水平恒力F向右推，使滑块做匀加速运动，在2s后撤去推力F，滑块再运动3s时经过B点，已知AB间距x0=49m，（已知sin37°=0.6，cos37°=0.8）．求： （1）刚撤去推力F时滑块的加速度大小； （2）推力F的大小．  |
◎ 答案
| （1）刚撤去F后，根据牛顿第二定律得， mgsin37°+μmgcos37°=ma2． 代入数据，解得a2=10m/s2． （2）在头2s内，滑块的位移x1＞v0t1=10×2m=20m． 后3s内，若始终向上减速运动，则x2＞
则x1+x2=65m＞49m，故后3s内滑块必定已经沿斜面向上运动到最高点后返回向下运动一段时间． Fcos37°-mgsin37°-μ（mgcos37°+Fsin37°）=ma1． 解得a1=0.5F-10． x1=v0t1+
得x1=20+2a1 v1=v0+a1t1 得，v1=10+2a1 x2=
解得x2=
t2=
得t2=
根据牛顿第二定律得，下滑时有：mgsin37°-μmgcos37°=ma3． 代入数据解得a3=2m/s2． x3=
|
