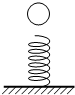
如图所示,竖直放置的质量为4m、长为L的圆管顶端塞有一个可看作质点的弹性圆球,弹性圆球的质量为m,球和管间的滑动摩擦力和最大静摩擦力大小均为4mg.圆管从下端离地面距离为
◎ 题目
| 如图所示,竖直放置的质量为4m、长为L的圆管顶端塞有一个可看作质点的弹性圆球,弹性圆球的质量为m,球和管间的滑动摩擦力和最大静摩擦力大小均为4mg.圆管从下端离地面距离为H处自由下落,落地后向上弹起的速度与落地速度大小相等.试求: (1)圆管底端落地前瞬间的速度; (2)圆管弹起后圆球不致滑落,L应满足什么条件. (3)圆管上升的最大高度是多少?  |
◎ 答案
| (1)取竖直向下为正方向,则: 根据v02=2gH得, 圆管第一次碰地前的瞬时速度v0=
(2)碰地后瞬间,管的速度v管=-
碰后,管受重力作用及向下的摩擦力作用,加速度a管=2g;球受重力和向上的摩擦力作用,加速度a球=-3g.球相对管的加速度a相=-5g. 以管为参考系,则球与管相对静止前,球相对管下滑的距离为: s相1=
要使球不滑出圆管,应满足:L>s相1=
(3)设管从碰地到它弹到最高点所需时间为t1(设球与管这段时间内摩擦力方向不变),则: t1=
|