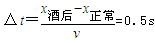一位滑雪者收起雪杖自由滑行,他以v0=40m/s的初速度自雪坡底端O点沿直线冲上雪坡,速度减到0后仍不用雪仗立即转身又自由滑下(忽略转身时间),已知雪坡足够长,雪坡倾角为θ=3
◎ 题目
| 一位滑雪者收起雪杖自由滑行,他以v0=40m/s的初速度自雪坡底端O点沿直线冲上雪坡,速度减到0后仍不用雪仗立即转身又自由滑下(忽略转身时间),已知雪坡足够长,雪坡倾角为θ=37°,雪橇与雪坡间的动摩擦因数μ=0.5,从滑雪者刚滑上雪坡O点开始计时,取g=10m/s2,sin37°=0.6,cos37°=0.8. (1)求人能沿雪坡向上滑行的最大距离. (2)雪坡上距底端75m远处有一点P,求从计时开始人滑到P点所需时间.  |
◎ 答案
| (1)滑雪者沿斜面向上运动时沿斜面方向受到重力的分力和摩擦力的作用,根据牛顿第二定律可得人的加速度: a1=g(sin37°+ucos37°)=10m/s2 上升时人做减速运动,则根据匀变速直线运动的速度位移关系有: 0-
得人上升的最大距离x=
(2)滑雪者沿斜面向上运动的总时间为t: 由速度时间关系为: 0=v0-a1t 得人上滑的时间t=
若P点为沿斜面向上运动时所经过的时间为t1,则由 位移时间关系有:xp=v0t1-
代入数据可解得:t1=3s 若P点为沿斜面向下运动时所经过的,则滑雪者沿斜面向下运动时的加速度大小: a2=g(sin37°-ucos37°)=2m/s2 上滑到最高点又回到p点所走的位移为:s=x-xp=5m 由位移时间关系有物体由最高点下滑至P点所用时间为t2: s=
得t2=
|