如图所示，在倾角θ＝30o的斜面上放置一段凹槽B，B与斜面间的动摩擦因数μ＝，槽内靠近右侧壁处有一小物块A(可视为质点)，它到凹槽左侧壁的距离
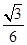d＝0.10m。A、B的质量都为m=2.0kg，B与斜面间的最大静摩擦力可认为等于滑动摩擦力，不计A、B之间的摩擦，斜面足够长。现同时由静止释放A、B，经过一段时间，A与B的侧壁发生碰撞，碰撞过程不计机械能损失，碰撞时间极短。取g=10m/s²。求：

（1）画出凹槽B运动的速度v随时间t的变化图象；
（2）物块A与凹槽B的左侧壁第n次碰撞后瞬间A、B的速度大小；
（3）从初始位置到物块A与凹槽B的左侧壁发生第n次碰撞时B的位移大小。

（1）（2）v_An=(n-1)m?s^-1，v_Bn="n" m?s^-1（3）x_n总=0.2n²m

试题分析：：（1）槽所受的最大静摩擦力等于重力沿斜面的分力，所以物块释放后，槽处于静止，物块做匀加速直线运动，根据位移时间公式求出小球与槽壁第一次发生碰撞时所需的时间．
（2）物块和槽发生碰撞的前后瞬间，动量守恒，能量守恒，根据动量守恒定律和能量守恒定律求出槽和小球的速度．
（3）第一次碰撞后，槽做匀速运动，物块做匀加速运动，在运动的过程中，开始时槽的速度大于球的速度，物块与A壁的距离越来越大，速度相等时，物块到侧壁B的距离最大，判断此时是否与A壁相碰，若没相碰，此后的物块与A壁的距离越来越小，抓住位移相等，求出追及的时间．
解：（1）A在凹槽内，B受到的滑动摩擦力       ①
B所受重力沿斜面的分力
因为，所以B受力平衡，释放后B保持静止 ②
释放A后，A做匀加速运动，由牛顿定律和运动学规律得
     ③
                             ④
解得A的加速度和碰撞前的速度分别为：      ⑤
B发生碰撞时运动的时间：，
动量守恒                ⑥
碰撞过程不损失机械能，得           ⑦
解得第一次发生碰撞后瞬间A、B的速度分别（方向沿斜面向下）       ⑧
之后B匀速运动，A加速运动，A、B第一次碰撞后，B做匀速运动
                                   ⑨
A做匀加速运动，加速度仍为a₁
                                 ⑩
                                    ?
经过时间t₁，A的速度与B相等，A与B的左侧壁距离达到最大，即
                                  ?
                                  ?
代入数据解得A与B左侧壁的距离
s=0.10m                                 ?
因为s=d， A恰好运动到B的右侧壁，而且速度相等，所以A与B的右侧壁恰好接
触但没有发生碰撞。再次相碰的时间为：，得到：t=0.4s，此时A的速度为：
动量守恒               
碰撞过程不损失机械能，得         
解得：（方向沿斜面向下） 
同理可以求出：（方向沿斜面向下）

（2）由以上分析可知：物块A与凹槽B的左侧壁第n次碰撞后瞬间A、B的速度大小分别为：v_An=(n-1)m?s^-1，v_Bn="n" m?s^-1
（3）由以上分析可知：从初始位置到物块A与凹槽B的左侧壁发生第n次碰撞时B的位移大小：
点评：本题难度较大, 本题综合运用了牛顿第二定律、动量守恒定律和能量守恒定律，综合性较强，关键是理清球与槽的运动情况，选择合适的规律进行求解,对运动过程的把握要强,选择合适的知识点求解也非常关键