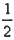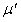一固定的斜面,倾角为45°,斜面长L=2.0米,在斜面下端有-与斜面垂直的挡板.一质量为m的滑块,从斜面的最高点沿斜面下滑,初速度为零.滑块沿斜面下滑到斜面最低端与挡板发生
◎ 题目
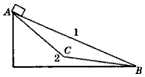
| 一固定的斜面,倾角为45°,斜面长L=2.0米,在斜面下端有-与斜面垂直的挡板.一质量为m的滑块,从斜面的最高点沿斜面下滑,初速度为零.滑块沿斜面下滑到斜面最低端与挡板发生弹性碰撞(碰撞前后能量没有损失).已知滑块与斜面间的滑动摩擦系数μ=0.2.试求: (1)滑块与挡板发生第1次碰撞时的速度大小及反弹后上升的最大距离? (2)此滑块从开始运动到与挡板发生第5次碰撞前的过程中运动的总路程.  |
◎ 答案
(1)由动能定理得mgLsinθ-fL=
且f=μmgcosθ ② 由①②得 v1=
滑块向上运动由动能定理得-mgL1sinθ-fL1=0-
由方程①②③得
所以反弹后上升的最大距离为
(2)令α=
同理第2次碰撞后上升的距离为L2=αL1=α2L 第3次碰撞后上升的距离为L3=αL2=α3L … 第1次碰撞前通过的路程s1=L 第2次碰撞前通过的路程s2=L+2L1=L+2αL 第3次碰撞前通过的路程s3=L+2L1+2L2
上一篇:蹦级是一种极限体育项目,可以锻炼人的胆量和意志,运动员从高处跳下,弹性绳被拉展前做自由落体运动,弹性绳被拉展后在弹性的缓冲作用下,运动员下落一定高度后速度减为零.
下一篇:蹦床是跳水运动员日常训练时的重要辅助器材.一个运动员从高处落到蹦床上后又被弹起到原高度,利用仪器测得该运动员从高处开始下落到弹回的整个过程中,运动速度随时间变化的
零零教育社区:论坛热帖子
|