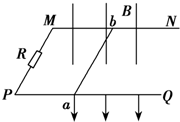
如图甲所示,两根足够长的光滑平行金属导轨相距为L=0.40m,导轨平面与水平面成θ=30?角,上端和下端通过导线分别连接阻值R1=R2=1.2Ω的电阻,质量为m=0.20kg、阻值为r=0.2
,m=0.2kg,R=1.2Ω,r=0.20Ω,θ=30°
可计算得F=
+
.
(4)令通过导体棒的电流为I,则通过电阻R1和R2的电流分别为
I
电流做功Q=I2Rt得:
对于R1产生的热量:Q1=(
)2Rt
对于R2产生的热量:Q2=(
)2Rt
对于导体棒r产生的热量:Q3=I2rt
因为I和t相等,R=1.2Ω,r=0.2Ω,Q1=0.135J
所以可以计算出:Q2=Q1=0.135J,Q3=0.09J
即整个电路产生的热量Q=Q1+Q2+Q3=0.36J
对整个0.5s过程中由于导体棒的加速度为
m/s2在0.5s的时间里,导体棒沿轨道上升的距离
x=
at2=
×
×(
)2m=
m
0.5s末导体棒的速度v=at=
×
m/s=
m/s
在这0.5s的时间里,满足能量守恒,故有:
WF-Q-mgxsinθ=
mv2
∴力F做功为:WF=Q+mgxsinθ+
mv2
代入Q=0.36J,m=0.2kg,x=
m,v=
m/s可得:
WF=2.34J
答:(1)磁感应强度B=1T;
(2)在0-0.5s时间内金属棒的加速度a=
m/s2;
(3)在0-0.5s时间内电动机牵引力F与时间t的关系:F=
可计算得F=
| 4t |
| 3 |
| 7 |
| 3 |
(4)令通过导体棒的电流为I,则通过电阻R1和R2的电流分别为
| 1 |
| 2 |
电流做功Q=I2Rt得:
对于R1产生的热量:Q1=(
| I |
| 2 |
对于R2产生的热量:Q2=(
| I |
| 2 |
对于导体棒r产生的热量:Q3=I2rt
因为I和t相等,R=1.2Ω,r=0.2Ω,Q1=0.135J
所以可以计算出:Q2=Q1=0.135J,Q3=0.09J
即整个电路产生的热量Q=Q1+Q2+Q3=0.36J
对整个0.5s过程中由于导体棒的加速度为
| 20 |
| 3 |
x=
| 1 |
| 2 |
| 1 |
| 2 |
| 20 |
| 3 |
| 1 |
| 2 |
| 5 |
| 6 |
0.5s末导体棒的速度v=at=
| 20 |
| 3 |
| 1 |
| 2 |
| 10 |
| 3 |
在这0.5s的时间里,满足能量守恒,故有:
WF-Q-mgxsinθ=
| 1 |
| 2 |
∴力F做功为:WF=Q+mgxsinθ+
| 1 |
| 2 |
代入Q=0.36J,m=0.2kg,x=
| 5 |
| 6 |
| 10 |
| 3 |
WF=2.34J
答:(1)磁感应强度B=1T;
(2)在0-0.5s时间内金属棒的加速度a=
| 20 |
| 3 |
(3)在0-0.5s时间内电动机牵引力F与时间t的关系:F=

![静止在粗糙水平面上的物体,受到水平方向的拉力作用由静止开始运动,在0~6s内其速度与时间图象和拉力的功率与时间图象如图所示,则物体的质量为(取g=10m/s2)[]A.B.C.D.](http://www.00-edu.com/d/file/2022-11-05/7ecc2d612ea73e5ffeff90deeb431a0b.gif)