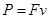如图甲所示,间距为L=0.3m、足够长的固定光滑平行金属导轨MN、PQ与水平面成θ=30°角,左端M、P之间连接有电流传感器和阻值为R=0.4Ω的定值电阻.导轨上垂直停放一质量为m=0.
由牛顿第二定律得:F-F安-mgsinθ=ma
则此时的外力:F=F安+mgsinθ+ma=7.5×10-2N+0.1×10×0.5N+0.1×1N=0.675N
则功率:P=Fv=0.675×2W=1.35W
答:(1)2s时刻杆ab的速度υ大小为2m/s.
(2)加速度a的大小为1m/s2.
(3)从静止开始在2秒内通过金属杆ab横截面的电量q为0.5C.
(4)2s时刻外力F的功率P为1.35W.
◎ 解析
“略”◎ 知识点
专家分析,试题“如图甲所示,间距为L=0.3m、足够长的固定光滑平行金属导轨MN、PQ与水平面成θ=30°角,左端M、P之间连接有电流传感器和阻值为R=0.4Ω的定值电阻.导轨上垂直停放一质量为m=0.…”主要考查了你对 【牛顿第二定律】,【平均功率和瞬时功率的区别】,【导体切割磁感线时的感应电动势】,【电磁感应现象中的磁变类问题】,【电磁感应现象中的切割类问题】 等知识点的理解和应用能力。关于这些知识点的“档案”,你可以点击相应的链接进行查看和学习。- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
上一篇:电动自行车具有低噪声、无废气、无油污的环保性,而且它的能源利用率很高.下表列出了某品牌电动自行车及所用电动机的主要技术参数,不计其自身机械损耗.若该车在额定状态下以
下一篇:放在水平地面上的物体,受到水平拉力F的作用,在0至6s内其速度图线和F的功率图线如图所示,则物体的质量约为()A.1.67kgB.0.6kgC.0.9kgD.1.1kg
零零教育社区:论坛热帖子
| [高考] 2022 西安电子科技大学《软件工程》大作业答案 (2022-04-25) |
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |

![静止在粗糙水平面上的物体,受到水平方向的拉力作用由静止开始运动,在0~6s内其速度与时间图象和拉力的功率与时间图象如图所示,则物体的质量为(取g=10m/s2)[]A.B.C.D.](http://www.00-edu.com/d/file/2022-11-05/7ecc2d612ea73e5ffeff90deeb431a0b.gif)