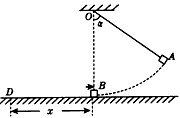
如图所示,在E=103V/m的水平向左匀强电场中,有一光滑半圆形绝缘轨道竖直放置,轨道与一水平绝缘轨道MN连接,半圆轨道所在竖直平面与电场线平行,其半径R=40cm,一带正电荷q
◎ 题目
| 如图所示,在E=103V/m的水平向左匀强电场中,有一光滑半圆形绝缘轨道竖直放置,轨道与一水平绝缘轨道MN连接,半圆轨道所在竖直平面与电场线平行,其半径R=40cm,一带正电荷q=10-4C的小滑块质量为m=40g,与水平轨道间的动摩擦因数μ=0.2,取g=10m/s2,问: (1)要小滑块能运动到圆轨道的最高点C,滑块应在水平轨道上离N点多远处释放? (2)这样释放的滑块通过P点时对轨道压力是多大?(P为半圆轨道中点) (3)小滑块经过C点后最后落地,落地点离N点的距离多大?落地时的速度是多大?  |
◎ 答案
| (1)设滑块与N点的距离为L, 分析滑块的运动过程,由动能定理可得, qEL-μmgL-mg?2R=
小滑块在C点时,重力提供向心力, 所以 mg=m
代入数据解得 v=2m/s,L=20m. (2)滑块到达P点时,对全过程应用动能定理可得, qE(L+R)-μmgL-mg?R=
在P点时由牛顿第二定律可得, N-qE=m
解得N=1.5N 由牛顿第三定律可得,滑块通过P点时对轨道压力是1.5N. (3)小滑块经过C点,在竖直方向上做的是自由落体运动, 由2R=
t=
滑块在水平方向上只受到电场力的作用,做匀减速运动, 由牛顿第二定律可得 qE=ma, 所以加速度 a=2.5m/s2, 水平的位移为 x=vt-
代入解得 x=0.6m. 滑块落地时竖直方向的速度的大小为vy=gt=10×0.4m/s=4m/s, 水平方向的速度的大小为 vx=v-at=2-2.5×0.4=1m/s, 落地时速度的大小为v地=
|


![质量为1500kg的汽车在平直的公路上运动,v-t图象如图所示。由此不可求出的下列物理量是[]A.前25s内汽车的平均速度B.前l0s内汽车的加速度C.前l0s内汽车所受的阻力D.15~25s内合](http://www.00-edu.com/d/file/2022-11-05/6634ddaad6711d5db061211ee3b3344b.gif)
![质量为1500kg的汽车在平直的公路上运动,v-t图象如图所示。由此可求[]A.前25s内汽车的平均速度B.前10s内汽车的加速度C.前10s内汽车所受的阻力D.15~25s内台外力对汽车所做](http://www.00-edu.com/d/file/2022-11-05/2d11ece61cc5126253c6d5ed0aa8059b.gif)
