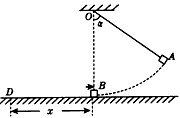
如图所示,在以O为圆心,半径为R=103cm的圆形区域内,有一个水平方向的匀强磁场,磁感应强度大小为B=0.10T,方向垂直纸面向外.竖直平行放置的两金属板A、K相距为d=203mm,连
◎ 题目
如图所示,在以O为圆心,半径为R=10
问:(1)请分段描述正离子自S1到荧光屏D的运动情况. (2)如果正离子垂直打在荧光屏上,电压表的示数多大? (3)调节滑动变阻器滑片P的位置,正离子到达荧光屏的最大范围多大?  |
◎ 答案
| (1)正离子在两金属板间受到电场力而作匀加速直线运动,离开电场后做匀速直线运动,进入磁场后受到洛伦兹力而做匀速圆周运动,离开磁场后,离子又做匀速直线运动,直到打在荧光屏上. (2)设离子由电场射出后进入磁场时的速度为v.因离子是沿圆心O的方向射入磁场,由对称性可知,离子射出磁场时的速度方向的反向延长线也必过圆心O.离开磁场后,离子垂直打在荧光屏上(图中的O′点),则离子在磁场中速度方向偏转了90°,由几何知识可知,离子在磁场中做圆周运动的半径 r′=R=10
设离子的电荷量为q、质量为m,进入磁场时的速度为v有 由qvB=m
设两金属板间的电压为U,离子在电场中加速,由动能定理有: qU=
而
由②③两式可得U=
代入有关数值可得U=30V,也就是电压表示数为30V. (3)因两金属板间的电压越小,离子经电场后获得的速度也越小,离子在磁场中作圆周运动的半径越小,射出电场时的偏转角越大,也就越可能射向荧光屏的左侧. 由闭合电路欧姆定律有,I=
当滑动片P处于最右端时,两金属板间电压最大,为Umax=I(R1+R2)=90V 当滑动片P处于最左端时,两金属板间电压最小,为Umin=IR1=10V 两板间电压为Umin=10V时,离子射在荧光屏上的位置为所求范围的最左端点,由②③可解得离子射出电场后的速度大小为v1=2×103m/s,离子在磁场中做圆运动的半径为r1=0.1m. 此时粒子进入磁场后的径迹如图答2所示,O1为径迹圆的圆心,A点为离子能射到荧光屏的最左端点.由几何知识可得: tan
|


![质量为1500kg的汽车在平直的公路上运动,v-t图象如图所示。由此不可求出的下列物理量是[]A.前25s内汽车的平均速度B.前l0s内汽车的加速度C.前l0s内汽车所受的阻力D.15~25s内合](http://www.00-edu.com/d/file/2022-11-05/6634ddaad6711d5db061211ee3b3344b.gif)
![质量为1500kg的汽车在平直的公路上运动,v-t图象如图所示。由此可求[]A.前25s内汽车的平均速度B.前10s内汽车的加速度C.前10s内汽车所受的阻力D.15~25s内台外力对汽车所做](http://www.00-edu.com/d/file/2022-11-05/2d11ece61cc5126253c6d5ed0aa8059b.gif)
